5). Сила упругости
Сила упругости — это сила, упр,, возникающая в результате деформации тела и стремящаяся восстановить прежние размеры и форму тела.
Связь между силой упругости и упругой деформацией тела была установлена английским физиком Гуком.
Закон Гука
Закон Гука для одностороннего растяжения (сжатия) формулируют так:
сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела:
Fупр
=
,
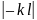Рис. 37.
Сила упругости направлена противоположно деформации.
Жесткость пружины численно равна силе, которую надо приложить к упруго деформируемому образцу, чтобы вызвать его единичную деформацию.
В
СИ:
.
Коэффициент жесткости зависит от формы и размеров тела, а также от материала.
При последовательном соединении, например, двух пружин жесткость рассчитывается по формуле:
При параллельном соединении пружин их жесткость равна:
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
4.4. Импульс. Закон сохранения импульса
И́мпульс (количество движения) — векторная физическая величина, являющаяся мерой механического движения тела.
В классической механике импульс материальной точки равен произведению массы m точки на её скорость , направление импульса совпадает с направлением вектора скорости (рис. 38): = m .
Рис. 38.
В
СИ: [P]
=
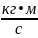или
(Н•с).
В
классической
механике
полным
импульсом
системы материальных
точек
называется векторная величина, равная
сумме произведений масс материальных
точек на их скорости:
=
.
соответственно
величина
=
mi
называется импульсом одной материальной
точки. Это векторная величина, направленная
в ту же сторону, что и скорость частицы.
Если мы имеем дело с телом конечного
размера, не состоящим из дискретных
материальных точек, для определения
его импульса необходимо разбить тело
на малые части, которые можно считать
материальными точками и просуммировать
по ним, в результате получим:
=
dx
dy
dz.
В
релятивистской
механике
(
трёхмерным импульсом системы
невзаимодействующих материальных точек
называется величина:
=
,
где mi — масса i-й материальной точки.
История появления термина
Рис. 39. Декарт (Descartes) Рене (латинизированное — Картезий; Cartesius) (1596-1650), французский философ, математик, физик и физиолог, и философ, создатель знаменитого метода координат.
Ещё в первой половине XVII века понятие импульса введено Рене Декартом (рис.39). Так как физическое понятие массы в то время отсутствовало, он определил импульс как произведение «величины тела на скорость его движения». Позже такое определение было уточнено Исааком Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».
Закон сохранения импульса
В
инерциальной системе отсчёта импульс
замкнутой системы частиц остаётся
постоянным:
const.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Из определения закона сохранения импульса следует, что он строго выполняется лишь в идеальном случае.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной из фундаментальных симметрий, — однородность пространства9.