3.4Расчет напряжений в хвостовике лопатки.
Тип хвостовика рассматриваемой лопатки – ёлочка (рис. 11). Для расчета разделим хвостовик на пять участков.
Рис. 11 Хвостовик.
Рис. 12 Зуб хвостовика.
Величина нагрузки Q прикладывается в середине отрезка СМ и перпендикулярно ему. При условии, что bi = const
,
(50)
где n – число зубьев; Nр –сила растяжения пера лопатки в корневом сечении; NХВ – центробежная сила хвостовика.
Н.
Сила, действующая на хвостовик в пяти полученных участках
,
(52)
где Vi – объем i-го участка; RСР.i – средний радиус участка хвостовика.
Н.
Напряжение смятия на поверхности СМ:
,
(53)
МПа.
Условие прочности выполняется:
МПа.
Напряжение изгиба в сечении АВ
,
(54)
МПа.
Условие прочности:
МПа.
Напряжение среза в сечении СD
,
(55)
МПа.
Условие прочности
МПа.
Напряжения растяжения в сечении 1-1
,
(56)
где
,
(57)
,
(58)
м2,
Н.
МПа.
Условие прочности
МПа.
Напряжение растяжения в сечении 2-2
,
(59)
,
(60)
,
(61)
м2,
МПа.
Условие прочности выполняется:
МПа.
3.5Расчет колебаний лопатки.
3.5.1Определение собственной частоты колебаний лопатки без учета вращения.
Собственная круговая частота изгибных колебаний лопатки без учета вращения:
,
(62)
где
λ
– безразмерный коэффициент; l
– длина лопатки; Е
– модуль упругости; ρЛ
– плотность лопатки;
-максимальная
толщина корневого сечения.
,
(63)
где р – собственная частота колебаний лопатки.
Параметр закрученности:
где
b
-
хорда лопатки;
полный
угол закрученности, град.
Относительные параметры:
относительная
изогнутость корневого сечения;
максимальная
толщина периферийного сечения;
максимальная
стрела изогнутости периферийного
профиля;
Теперь, из таблицы 1 пособия [4] определяются:
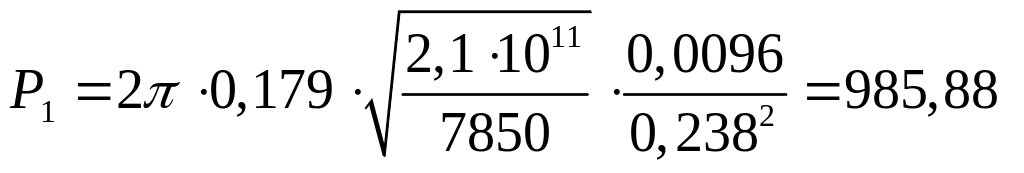рад/с.
Гц.
3.5.2Определение собственных частот с учетом вращения.
В поле центробежных сил лопатка ужесточается, ее собственная частота изгибных колебаний возрастает.
Собственная частота изгибных колебаний лопатки с учетом вращения
,
(69)
где
.
(70)
.
Задавшись значениями nСЕК , строим диаграмму Кэмпбелла.
Рис. 14 Частотная диаграмма Кэмпбелла.
Таблица 13. Расчет первой и второй собственных частот лопатки в зависимости от частоты вращения.
-
n, об/сек
f1, Гц
f2, Гц
0
156,90
418,13
10
157,97
418,53
20
161,13
419,74
30
166,27
421,73
40
173,21
424,52
50
181,73
428,07
55
186,53
430,13
60
191,65
432,37
70
202,73
437,40
80
214,82
443,13
90
227,74
449,53
100
241,37
456,59
110
255,58
464,26
120
270,29
472,52
130
285,43
481,34
140
300,92
490,68
150
316,71
500,52
160
332,77
510,83
170
349,05
521,59
180
365,53
532,75
190
382,18
544,31
200
398,97
556,23
210
415,90
568,49
220
432,94
581,08
230
450,08
593,96
Резонансная частота вращения ротора:
.
(71)
Для к = 3
об/с.
Расчет остальных резонансных оборотов приведен в таблице 14.
Таблица 14. Резонансные частоты оборотов.
к |
nРЕЗ, об/с |
2 |
196,74 |
3 |
66,09 |
4 |
44,14 |
5 |
33,73 |
6 |
27,46 |
Получив резонансные числа оборотов необходимо найти опасные зоны, в окрестностях которых резонанс все еще опасен. Для этого воспользуемся таблицей 15.
Таблица 15. Опасные зоны.
к |
± (n-nРЕЗ)/n·100% |
2 |
15 |
3 |
8 |
4 |
6 |
5 |
5 |
6 |
4 |
В табл. 15 представлены диапазоны опасных зон для различных К.
Таблица 15. Диапазоны опасных зон.
к |
Диапазон, об/с |
|
- |
от |
до |
2 |
167,23 |
226,25 |
3 |
60,80 |
71,38 |
4 |
41,49 |
46,79 |
5 |
32,04 |
35,42 |
6 |
26,37 |
28,56 |
об/с.
Из рис. 14 и таблицы 15 видно, что nРАБ не попадает в опасную зону, значит лопатка удовлетворяет требованиям вибронадежности.