4.2.Средняя гармоническая

Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической, исчисленной по тем же значениям признака. Как и средняя арифметическая, она может быть простой и взвешенной.

Пример 5.

Бригада рабочих была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.

На первый взгляд, кажется, что задача легко решается по формуле средней арифметической простой:

Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением:

все затраченное время

Среднее время, затраченное = --------------------------------------

на одну деталь число деталей

Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:

Это же решение можно представить иначе:

Таким образом, формула для расчета средней гармонической простой будет иметь вид:

Пример 6.

Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:

Таблица 4.4.-Группировка заводов по издержкам производства

Номер завода	Издержки производства, тыс.руб.	Себестоимость единицы продукции, руб.
1	200	20
2	460	23
3	110	22

Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.

Издержки производства

Средняя себестоимость = -----------------------------------

единицы продукции ( ) Количество продукции

руб.

Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:

4.3.Напараметрические средние

Характеристиками вариационных рядов, являются структурные или непараметрические средние, например: мода и медиана.

Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.

Пример 7.

Таблица 4.5. - Распределение проданной обуви по размерам

Размер обуви	36	37	38	39	40	41	42	43	44	45	и выше
Число пар, в % к итогу	—	1	6	8	22	30	20	11	1	1	—

В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.

Для интервальных рядов распределения с равными интервалами мода определяется по формуле:

где - начальное значение интервала, содержащего моду;

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

Пример 8.

Таблица 4.6.- Распределение предприятий по численности персонала

Группы предприятий по числу работающих, чел	Число предприятий
100 — 200	1
200 — 300	3
300 — 400	7
400 — 500	30
500 — 600	19
600 — 700	15
700 — 800	5
ИТОГО	80

В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.

Введем следующие обозначения:

=400, =100, =30, =7, =19

Подставим эти значения в формулу моды и произведем вычисления:

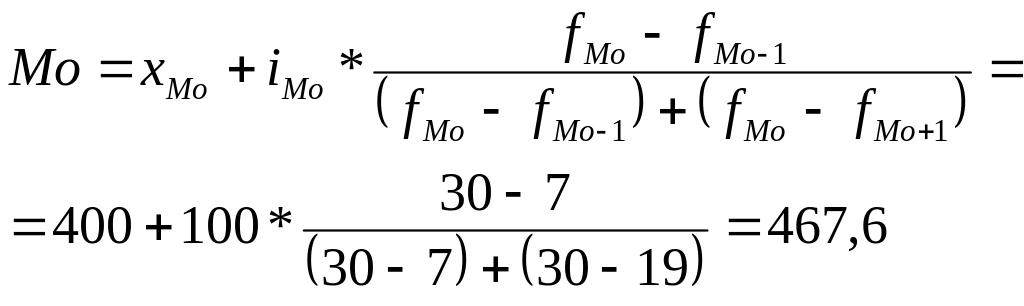
То есть в анализируемой совокупности наиболее часто встречаются предприятия со средней численностью 467,6 работников.

Медиана - это варианта, расположенная в середине вариационного ряда, которая отсекает 50 % значений. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).

Например, стаж пяти рабочих составил 2, 4, 7, 8, 10 лет. В таком упорядоченном ряду медиана - 7 лет. По обе стороны от нее находится одинаковое число рабочих.

Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять человек в бригаде, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда:

Ме = (6 + 7) / 2 = 6,5 лет.

Рассмотрим пример расчета медианы в дискретном ряду.

Пример 9.

Определим медиану заработной платы рабочих.

Таблица 4.7.-Расчет медианы заработной платы

Среднедневной заработок , руб.	Число рабочих	Сумма накопленных частот
110	2	2
130	6	8 (2+6)
160	16	24 (8+16)
190	12	—
220	4	—
	40

Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот равна 20. Варианта, соответствующая этой сумме, т.е. 160 руб., и есть медиана ряда.

Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.

Рассмотрим расчет медианы в интервальном вариационном ряду.

Медиана интервального вариационного ряда распределения определяется по формуле

где — начальное значение интервала, содержащего медиану;

— величина медианного интервала;

— сумма частот ряда;

— сумма накопленных частот, предшествующих медианному интервалу;

— частота медианного интервала.

Пример 10

По данным примера 8 ( табл.4.6.) определим максимальную численность рабочих на 50% предприятий.

Таблица 4.8.- Распределение предприятий по численности

Группы предприятий по числу рабочих	Число предприятий	Сумма накопленных частот
100 — 200	1	1
200 — 300	3	4 (1+3)
300 — 400	7	11 (4+7)
400 — 500	30	41 (11+30)
500 — 600	19	—
600 — 700	15	—
700 — 800	5	—
ИТОГО	80

Прежде всего, определим медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений равна 41, что соответствует интервалу 400 - 500. Это и есть медианный интервал, т.е. тот в котором находится медиана. Определим ее значение по приведенной выше формуле.

Известно, что:

Следовательно,

То есть в данной совокупности 50% предприятий имеют численность не более 496,66 рабочих.

Для еще более детального исследования структуры совокупности используют:

• квартили ( К_n ), отсекающие последовательно 1/4, 2/4, 3/4 значений совокупности или 25, 50 и 75 %. Методика расчета аналогична расчету медианы.

• децили ( D_n ), отсекающие последовательно 1/10, 2/10, 3/10 …n/10 значений совокупности. Методика расчета аналогична двум предыдущим показателям, поскольку D₅ = K₂ = M_e

Задания для самостоятельной работы

Задание №1.

По данным о распределении предприятий региона по товарообороту определите:

- средний объем товарооборота;

- моду;

- медиану.

По всем расчетам сделать выводы. Данные каждого расчета оформить в виде таблиц.

Таблица 4.9.- Распределение предприятий по объему товарооборота

Группы предприятий по объему товарооборота, млн.руб.	Число предприятий
до 400	9
400 — 500	12
500 — 600	8
600 — 700	9
свыше 700	2
Итого	40

Задание №2.

Заработная плата бригады строителей по отдельным профессиям за месяц характеризуется следующими данными:

Таблица 4.10.- Распределение рабочих по заработной плате

Маляры		Штукатуры		Кровельщики
Заработная плата, руб.	Число рабочих, чел.	Заработная плата, руб.	Число рабочих, чел.	Заработная плата, руб.	Число рабочих, чел.
200 210 217	1 1 1	220 236 240	2 2 2	230 242 255	3 5 2
Итого	3	-	6	-	10

Определите среднюю заработную плату рабочих по каждой профессии и в целом по бригаде.

Задание №3.

По данным обследования получены следующие данные:

Таблица 4.11- Распределение студентов-заочников по возрасту

Группа, № п/п	Группы студентов по возрасту, лет	Число студентов, чел.	Удельный вес студентов в группе
			в %	в коэффициентах
I II III IV	20 -25 25 -30 30 -35 35 -40	200 900 800 100	10 45 40 5	0,10 0,45 0,40 0,05
	Итого	2000	100	1,00

Определите средний возраст студентов-заочников.

Задание №4.

Средняя выработка продукции на одного рабочего за смену в двух цехах завода, вырабатывающих однородную продукцию, характеризуется следующими данными:

Таблица 4.12.- Распределение рабочих по средней выработке

Бригада, №	Цех № 1		Бригада, №	Цех № 2
	дневная выработка продукции, шт., x	число рабочих, чел.,		дневная выработка продукции, шт., x	объём произведённой продукции, шт., M
I II III	20 30 35	8 11 16	IV V VI	38 36 20	418 432 140

Определите среднедневную выработку продукции рабочих;

а) по первому цеху; б) по второму цеху.

Задание №5.

Имеются следующие данные о распределении операторов по затратам времени на обслуживание одного клиента:

Таблица 4.13.- Распределение работников по затратам времени

Затраты времени на одного клиента, мин.	Число операторов 1 подразделения, чел.	Число операторов 2 подразделения, чел
4,5-5,5 5,5-6,5 6,5-7,5 7,5-8,5 8,5-9,5 9,5-10,5 10,5-11,5	8 18 23 30 12 6 3	2 3 11 12 10 7 1

Определить моду и медиану времени обслуживания по первому и второму подразделениям.