1.1. Двумерные течения.

В общем случае в каждый момент времени поле скоростей потока жидкости определяется тремя функциями - - компонентами вектора скорости в некоторой криволинейной системе координат .

Поток, который может быть отнесен к такой координатной системе, что-бы все три компоненты скорости - - в каждый момент времени являлись функциями только двух координат - - и не зависели от третьей — , т.е.

будем называть двумерным. Геометрически это означает, что на всех координатных поверхностях поле скоростей строится одинаковым образом. Иначе говоря,

Отсюда вытекает, что якобиан от составляющих скорости по координатам

тождественно равен нулю

Следовательно, между функциями должно существовать соотношение, не зависящее от координат , т.е. при двумерном движении имеет место функциональная зависимость

которая позволяет одновременно с уменьшением числа переменных в уравнениях движения сократить число уравнений в системе.

1.2. Одномерные течения.

По аналогии с двумерными течениями одномерными потоками назовем течения, которые могут быть отнесены к такой координатной системе, в которой компоненты скорости будут функциями одной координаты ,

Очевидно, что все рассмотренные примеры двумерных течений в предположении (1.4) могут быть существенно упрощены. Из всего множества возможных случаев перехода от двумерных потоков к одномерным ограничимся рассмотрением двух важных примеров с постоянным распределением завихренности.

1. Пусть скорость плоскопараллельного установившегося течения в инерциальной системе координат имеет только одну составляющую вдоль оси и она будет функцией только одной координаты . Тогда имеем

Отсюда , где - скорость на оси . Следовательно, рассматриваемое течение обладает скоростью, которая по линейному закону меняется вдоль оси . Функция тока такого течения имеет вид

Это течение изображено на рис. 1.8 и называется сдвиговым течением. В частном случае ( ) все частицы жидкости движутся с одинаковыми постоянными скоростями . Такое движение называется однородным.

2. Пусть имеется установившееся течение с постоянной величиной завихренности, которое в цилиндрической системе координат имеет только одну окружную составляющую , зависящую от радиальной координаты . Записав в цилиндрической системе координат, с учетом сделанных предположений получим

После интегрирования находим

Для течений с ограниченными скоростями константу следует положить равной нулю. Линиями тока такого течения являются концентрические окружности (на схеме квазитвердого вращения жидкости), а окружная скорость меняется по линейному закону вдоль радиуса. Такое течение обычно называют квазитвердым вращением.

2. Исходные уравнения.

Система уравнений идеального изотермического газа применительно к атмосфере Земли в пренебрежении центробежной силой имеет следующий вид:

где - скорость; – ее модуль; – давление; - плотность; - плотность атмосферы у Земли; - единичный вектор вдоль оси вращения. Рассмотрение проводится в ортогональной системе координат .

Пусть течения однородные винтовые:

Здесь – параметр спиральности. Отметим, что уравнение неразрывности (2.2) является следствием уравнения (2.4). Действительно, применяя к левой и правой частям соотношения (2.4) операцию дивергенции, приходим к уравнению (2.2). С учетом уравнения (2.4) из уравнения движения (2.1) следует

Решая уравнение (5) относительно плотности, запишем

Как известно, для стандартной атмосферы в ее 70 - километровом (по толщине) слое абсолютная температура отличается от ее среднего значения не более, чем на . Далее примем для температуры , входящей в вышеприведенные соотношения, среднее значение температуры стандартной атмосферы по указанному слою, Наибольшие скорости, отмеченные в сильных циклонах, не превышают Поэтому выполнено неравенство

Следовательно, в выражении (2.6) множитель, включающий скорость, весьма мало отличается от единицы. В результате с погрешностью, не превышающей даже при , запишем

Полагая, найдем. В результате будем иметь

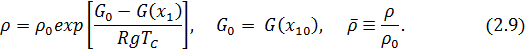
С учетом выражения (2.9) уравнениям (2.2) и (2.4) придадим следующий вид:

Положим

где – частное решение неоднородного уравнения (2.11). Подставляя (2.12) в уравнение (2.11), приходим к однородному уравнению для определения величины

Дальнейшее рассмотрение проведем в ортогональной системе координат коэффициенты Ламе которой удовлетворяют условиям:

В работах при изучении однородных винтовых течений жидкости постоянной плотности ( ) был введен следующий обобщенный потенциал S:

Здесь – оператор Лапласа; – орт, касательный координатной линии ; – заданная функция своего аргумента, выбираемая из соображения удобства. При этом рассмотрение также проводилось в ортогональной системе координат, коэффициенты Ламе которой удовлетворяют условиям (2.14).

Обобщая представление (2.15), будем разыскивать решение уравнения (2.13) в виде

где – обобщенный потенциал; величины – пока произвольные функции своего аргумента. Подставим выражение (2.16) для величины в уравнение (213). В результате запишем:

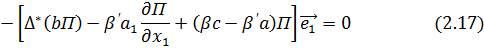
Здесь штрих означает дифференцирование соответствующей величины по своему аргументу. Приравнивая в соотношении (2.17) нулю коэффициенты при и ( ) под знаком градиента, коэффициент при под знаком ротора и множитель при в последнем слагаемом, соответственно запишем:

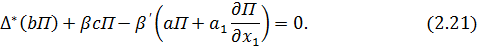
Далее для простоты положим

Тогда из соотношений (2.18) – (2.20) следует

Учтем выражения (2.22) – (2.25) в уравнении (2.21) и введем новый обобщенный потенциал следующим образом:

Здесь величина играет ту же роль, что и в соотношениях (2.15). В результате придeм к следующему уравнению:

Учитывая соотношения (1.22) – (1.26) в выражении для скорости (2.16), запишем

Таким образом, задача решения уравнения (2.13) в ортогональных координатах (2.14) сведена к линейному однородному дифференциальному уравнению в частных производных второго порядка (2.27), служащему для определения обобщенного потенциала S. Если этот обобщенный потенциал найден, то поле скорости определим с помощью выражения (2.28).

Отметим, что среди приведенных в курсе ортогональных координатных систем, в которых переменные в уравнении (2.27) разделяются, условиям (2.14) удовлетворяют прямоугольная система , три цилиндрических (круговая, эллиптическая и параболическая; ), а также сферическая и коническая системы

В указанных прямоугольных и трех цилиндрических системах координат удобно положить . В результате уравнение (2.27) принимает вид:

Здесь – оператор Лапласа. В случае сферической и конической систем координат удобно положить . В результате уравнение (2.27) принимает вид:

В пренебрежении силой Кориолиса рассмотрим потенциальные течения

Учитывая выражение (2.31) в уравнении неразрывности (2.10), получим следующее уравнение для потенциала Φ

Отметим, что в случае потенциальных течений выполнение условий (2.14) не обязательно.

Pассмотрение проводилось в предположении, что температура T атмосферы не зависит от высоты ( Это предположение является приближенным. Oтметим, что модели неизотермической атмосферы рассматривались в cравнительно недавней работе.