15.3. Понятие о двойных интегралах
Интегрирование функции на ограниченном множестве
Двойной интеграл от функции
,
подобно определенному интегралу,
определяется при помощи интегральных
сумм функции
.
Интегральные суммы функции
определялись на отрезке
.
Естественным обобщением отрезка в
пространстве
является замкнутая и ограниченная
область
.
Пусть на множестве
определена ограниченная функция
.
Рассмотрим разбиение
области
некоторыми
кривыми на
частичных областей
,
(рис.15.4). Диаметром
области
назовем наибольшее расстояние между
точками этой области, а размером разбиения
назовем наибольший среди диаметров
частичных областей :
.
В каждой частичной области
,
площадь которой обозначим символом
,
выберем точку
.
$$15.4
Определение 15.13. Сумма
называется интегральной суммой
функции
на области
.
Значение числа
зависит как от выбора разбиения
,
так и от выбора точек
.
Определение 15.14. Последовательность
разбиений
области
называется правильной, если
.
Числовая последовательность
называется последовательностью
интегральных сумм, если
последовательность разбиений
является правильной, а на выбор точек
не накладывается никаких ограничений.
Определение 15.15. Число
называется пределом интегральных
сумм
ограниченной функции
на области
,
если каждая последовательность
интегральных сумм
сходится к точке
.
Этот предел обозначают символом
.
Так как определение предела интегральных сумм сформулировано в терминах пределов последовательности, то это позволяет перенести основные результаты теории пределов на этот новый вид предела.
Определение 15.16. Число называется двойным интегралом функции
на области
,
его обозначают символом
,
функция
называется интегрируемой на
области
.
Из этого определение следует, что
.
Замечание. Функция , непрерывная на замкнутом и ограниченном множестве, интегрируема на этом множестве. ▲
Геометрическая интерпретация двойного интеграла
Пусть на области
задана непрерывная функция
,
которая на этой области принимает
неотрицательные значения. Криволинейным
цилиндром называется тело
в пространстве, ограниченное сверху
поверхностью
,
снизу — областью
,
а с боков — цилиндрической поверхностью,
образованной прямыми линиями, параллельными
оси
и проходящими через точки области
(рис. 15.15). Что называть объемом этого
тела?
$$15.5
Криволинейный цилиндр с основанием
(рис 15.5) заменим прямым цилиндром с
основанием
и высотой
.
Объем этого прямого цилиндра равен
.
Следовательно, интегральная сумма
представляет собой сумму объемов прямых
цилиндров, которая является приближенным
значением объема тела
.
Если существует предел
,
то его естественно считать объемом тела
.
Итак, объем
криволинейного цилиндра
с основанием
равен значению двойного интеграла
от неотрицательной и непрерывной функции
на области
,
т.е.
.
Замечание. Если существует
двойной интеграл
,
то он равен объему прямого цилиндра с
основанием
и высотой 1, т.е. равен площади
области
:
.
▲
Свойства двойных интегралов
Перечислим некоторые свойства двойных интегралов, которые аналогичны свойствам определенного интеграла.
1. Из интегрируемости функций
и
на множестве
следует интегрируемость функции
на этом множестве, причем
.
2. Если функции
и
интегрируемы на множестве
и справедливо неравенство
на этом множестве, то
.
3. Если функция
интегрируема на множествах
и
,
которые не имеют общих внутренних точек,
то
.
4. Если функция непрерывна в замкнутой и ограниченной области , то справедливо неравенство
.
Вычисление двойных интегралов
Самый простой способ вычисления двойного интеграла — сведение его к вычислению определенных интегралов. Этот способ можно реализовать, если область интегрирования является элементарной. Ниже перечисляются элементарные области интегрирования.
1.
— прямоугольная область, расположенная
между прямыми
,
,
,
а также между прямыми
,
,
,
и функция
непрерывна в этой прямоугольной области
,
то.
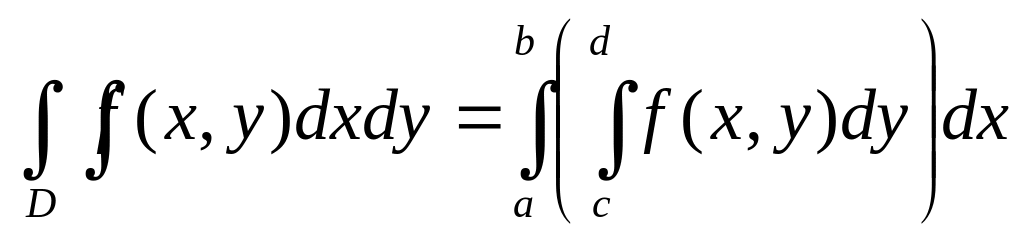
(15.3)
2. Область
расположена между прямыми
,
,
,
а также между непрерывными кривыми
,
(
,
).
Если функция
непрерывна в области
,
то
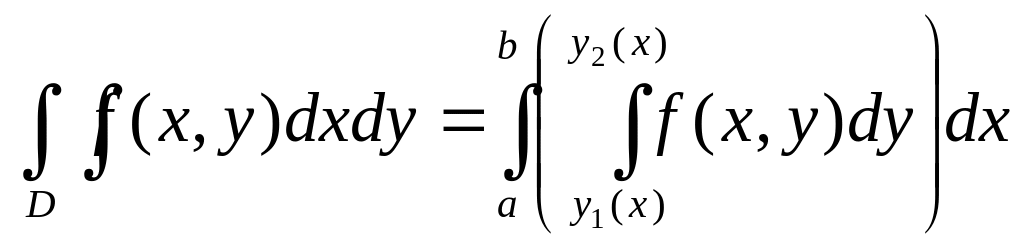(15.4)
3. Область
расположена между прямыми
,
,
,
а также между непрерывными кривыми
,
(
,
).
Если функция
непрерывна в области
,
то
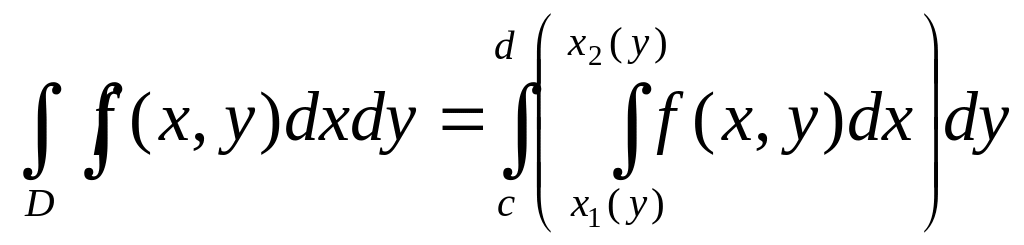(15.5)
Как вычислить двойной интеграл по области , которая не является элементарной? Надо область разбить прямыми, параллельными осям координат на конечное число непересекающихся элементарных областей. Затем, используя свойство 3 двойных интегралов, найти двойной интеграл по данной области .
Замечание. Правые части формул (15.3) – (15.4) называются повторными интегралами. Интеграл, стоящий в скобках, называется внутренним. Другой интеграл называется внешним. Сначала вычисляют внутренний интеграл, а затем вычисляют внешний интеграл. Вместо выражений
,
пишут соответственно
,
.
▲
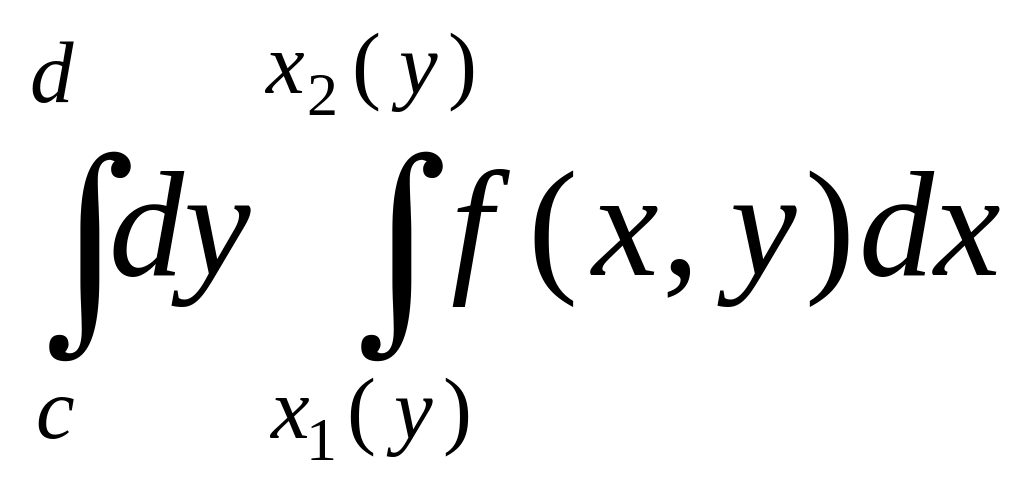Примеры
15.16. Вычислить повторный интеграл
.
Решение.
.
15.17. Вычислить двойной интеграл
по прямоугольной области
—
,
.
Решение. Применяя формулу (15.3), получим
.
15.18. Вычислить двойной интеграл
по области
,
ограниченной линиями
,
,
.
Решение. На рис. 15.6 изображена область . Она расположена между
$$15.6 $$15.7
прямыми
,
,
а также между линиями
и
.
Применяя формулу (15.5), получим
.
15.19. Вычислить двойной интеграл
по области
,
ограниченной линиями
,
,
.
Решение. На рис. 15.7 изображена область . Она расположена между
прямыми
,
,
а также между линиями
и
.
Применяя формулу (15.5), получим
.
15.20. Вычислить двойной интеграл
по области
,
ограниченной линиями
,
,
.
Решение. На рис. 15.8 изображена
область интегрирования
— треугольник
.
Она не является элементарной областью.
Разобьем область
прямой
на две элементарные области
и
(область
на рис. 15.8 показана черным цветом). Из
свойства 3 двойных интегралов следует
равенство
.
Вычислим эти интегралы.
$$15.8
.
.
Отсюда следует, что
.
●
Задачи
Вычислить повторные интегралы:
15.64.
.
15.65.
.
15.66.
.
15.67.
.
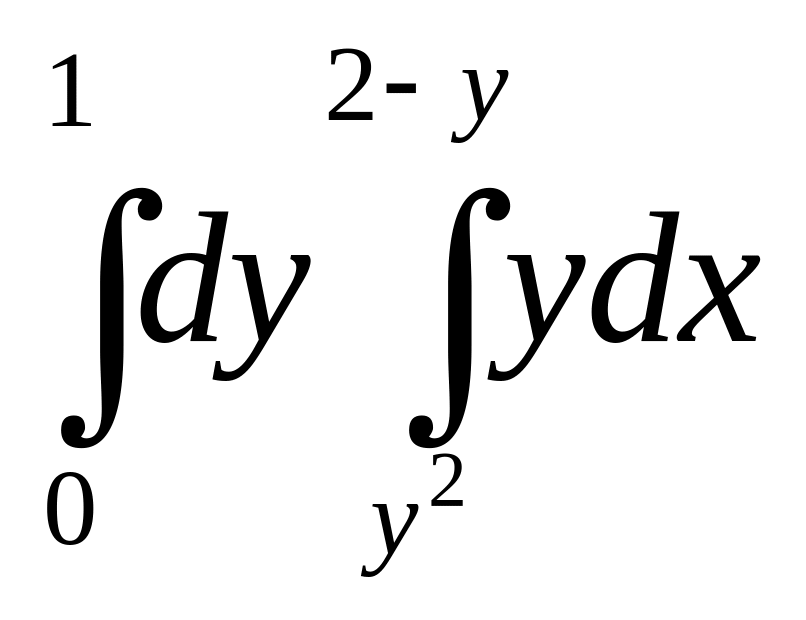15.68.
.
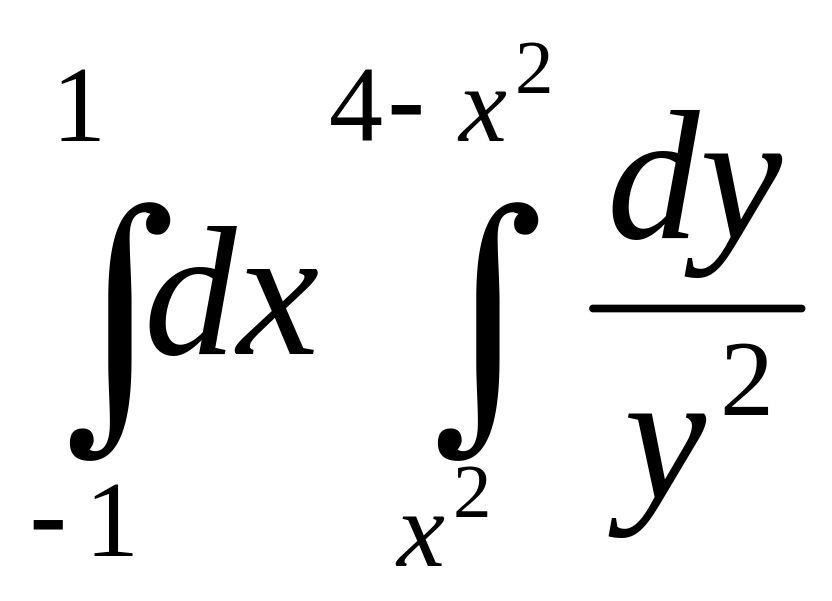Вычислить двойные интегралы по области , ограниченной линиями:
15.69.
,
.
15.70.
,
.
15.71.
,
.
15.72.
,
.
15.73.
,
.
15.74.
,
.
15.75.
,
,
неотрицательные части осей
и
.
15.76.
,
.
15.77.
,
.
15.78.
,
.
Ответы
15.64. 5. 15.65.
.
15.66.
.
15.67.
.
15.68.
.
15.69.
.
15.70.
.
15.71.
.
15.72.
.
15.73.
.
15.74.
.
15.75.
.
15.76.
.
15.77. 2. 15.78.
.
▲