15.3. Признаки сходимости несобственных интегралов

Лемма. Справедливы следующие утверждения.

1. Функция 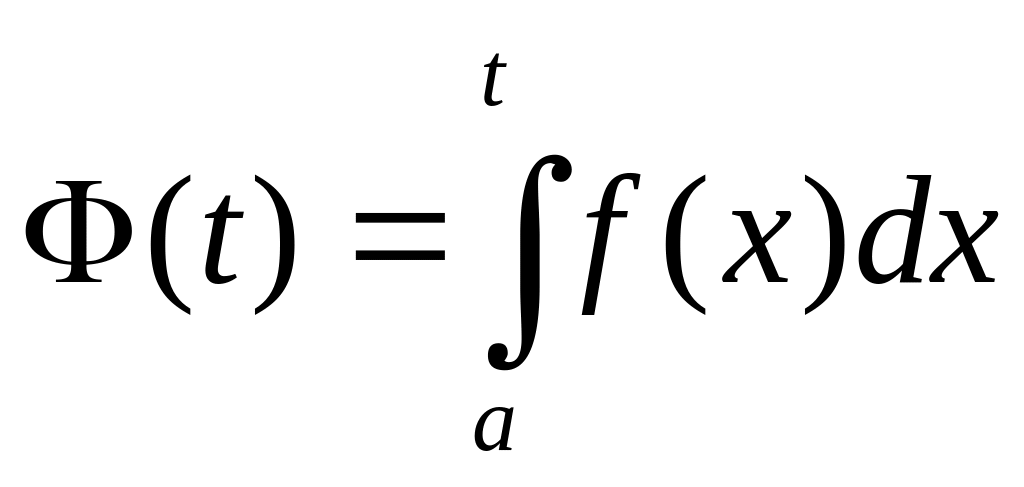является неубывающей, если функция

неотрицательна и интегрируема на отрезке .

2. Если неубывающая на отрезке функция ограничена

сверху, то существует предел , равный .

Доказательство

1. Если , то из 3-го и 4-го свойства определенного интеграла вытекает

.

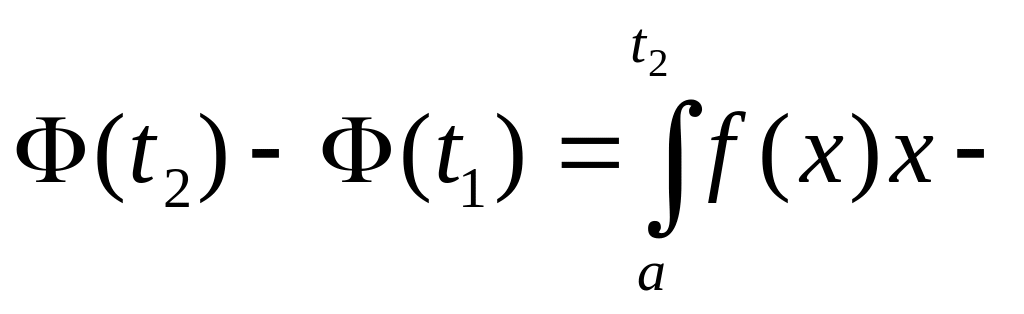
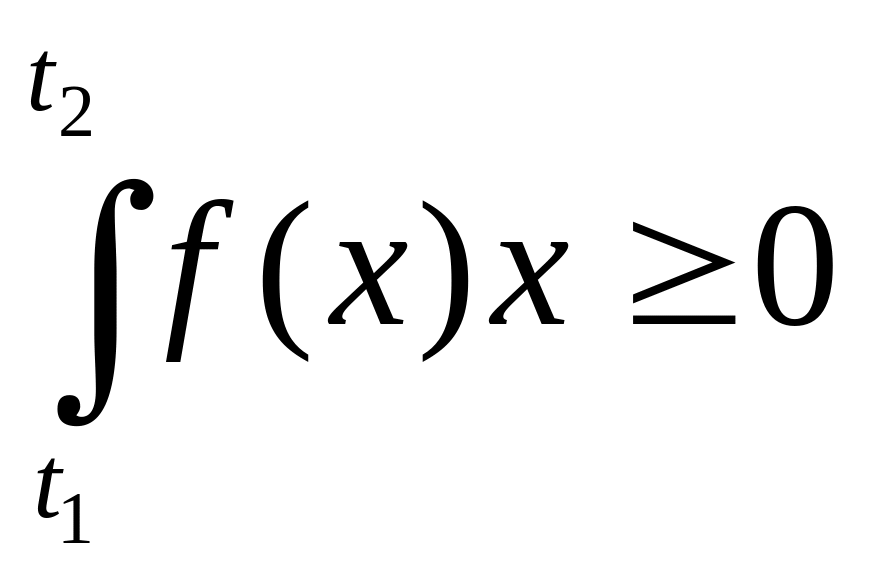2. Рассмотрим произвольную последовательность и докажем, что

. Из свойства точной верхней грани следует, что найдется такое значение функции , что , где . Так как , то найдется такое число , что , если . Теперь, из монотонности функции следует

.

Отсюда вытекает, что неравенство справедливо, если , т.е. . ■

Первый признак сходимости

Теорема 15.1. Если на промежутке выполняется неравенство , , то справедливы утверждения.

1. Из сходимости интеграла следует, что интеграл сходится.

2. Из расходимости интеграла следует, что интеграл расходится.

Доказательство

1. Если , то из условия и свойств интеграла получаем

.

Следовательно, функция ограничена сверху. Из 1-го утверждения леммы вытекает, что функция является неубывающей, а из 2-го утверждения этой леммы следует существование предела , т.е. интеграл сходится.

2. Доказательство проведем методом от противного, т.е. предположим, что

интеграл сходится. Тогда из первого утверждения теоремы следует сходимость интеграла . Противоречие. ■

Замечание. Теорема 15.1, останется справедливой, если в ее формулировке заменить промежуток промежутком и несобственные интегралы 1-го рода несобственными интегралами 2-го рода, подынтегральная функция которых неограничена в окрестности точки . ▲

Примеры

15.8. Доказать, что интеграл Эйлера-Пуассона сходится.

Решение. Так как на промежутке неравенство справедливо, и интеграл сходится, то из теоремы 15.1 следует, что интеграл сходится. Теперь из свойства 2 несобственных интегралов 1-го рода следует сходимость интеграла Эйлера-Пуассона.

15.9. Доказать сходимость несобственного интеграла .

Решение. Подынтегральная функция неограничена в окрестности нижнего предела интегрирования. Так как на промежутке неравенство справедливо, и интеграл сходится, то из замечания к теореме 15.1 следует, что интеграл сходится.

Доказать расходимость несобственных интегралов

15.10. . 15.11. .

Решение

15.10. Так как на промежутке неравенство справедливо, и интеграл расходится, то из теоремы 15.1 следует, что интеграл расходится.

15.11. Подынтегральная функция неограничена в окрестности верхнего

предела интегрирования. На промежутке неравенство справедливо. Так как интеграл расходится, то из замечания к теореме 15.1 следует, что интеграл расходится. ●

Задачи

Исследовать сходимость интегралов:

15.34. . 15.35. . 15.36. . 15.37. .

15.38. . 15.39. 15.40. . 15.41. .

15.42. . 15.43. .15.44. . 15.45. .

Исследовать на сходимость несобственные интегралы:

15.46. . 15.47. . 15.48. . 15.49. .

15.50. . 15.51. .

Ответы

15.34. сходится. 15.35. сходится. 15.36. расходится. 15.37. расходится. 15.38. сходится. 15.39. расходится. 15.40. сходится. 15.41. сходится. 15.42. сходится. 15.43. расходится. 15.44. сходится. 15.45. сходится. 15.46. сходится. 15.47. сходится. 15.48. расходится. 15.49. сходится. 15.50. сходится. 15.51. расходится. ▲

Второй признак сходимости

В некоторых случаях бывает затруднительно подобрать так функцию или , чтобы на требуемом промежутке было справедливо неравенство . Кроме того, необходимо, чтобы несобственный интеграл от функции сходился или несобственный интеграл от функции расходился. В этих случаях полезен второй признак сходимости несобственных интегралов. Сначала докажем лемму, необходимую далее.

Лемма. Если существует предел , , то функция ограничена на некотором промежутке , .

Доказательство проведем методом от противного. Тогда в каждом промежутке найдется такая точка , в которой . Так как последовательность — бесконечно большая и , то, . Отсюда и из определения предела функции следует, что . Следовательно, последовательность ограничена, что противоречит условию , . ■

Теорема 15.2. Пусть на промежутке функция , а функция и существует предел . Тогда интегралы и сходятся или расходятся одновременно.

Доказательство

1. Пусть сначала интеграл от функции сходится. Так как существует предел , , то из леммы следует ограниченность функции на некотором промежутке , , т.е. или , если . Из свойства 2 несобственных интегралов и условия теоремы следует, что интеграл сходится. Теперь из теоремы 15.1 вытекает сходимость интеграла , а из свойства 2 несобственных интегралов следует, что интеграл сходится.

2. Пусть интеграл сходится. Из условия теоремы следует, что . Теперь из 1-го утверждения доказательства теоремы вытекает сходимость интеграла .

3. Пусть интеграл от функции расходится. Докажем, что интеграл от функции расходится методом от противного. Если предположить, что интеграл от функции сходится, то из пункта 2 (1) доказательства теоремы следует сходимость интеграла от функции . Противоречие. ■

Теорема 15.3. Пусть на промежутке функция , а функция и существует предел . Тогда несобственный интегралы и сходятся или расходятся одновременно.

Доказательство проводится аналогично. ■

Замечание. Использовать 2-й признак сходимости несобственных интегралов можно следующим образом. Надо положить и подобрать так значение , чтобы предел . Затем определить при выбранном значении сходимость интеграла от функции . Из теорем 15.2 и 15.3 следует, что интегралы от функций и сходятся или расходятся одновременно. ▲

Примеры. Исследовать на сходимость следующие интегралы:

15.12. . 15.13. .

15.14. . 15.15. .

Решение

15.12. Подынтегральная функция и функция больше нуля на промежутке . Найдем предел частного этих функций, используя правило Лопиталя,

.

Так как интеграл сходится, то интеграл также сходится (теорема 15.2)

15.13. Подынтегральная функция и функция больше нуля на промежутке . Найдем предел частного этих функций, используя правило Лопиталя,

.

Так как интеграл расходится, то интеграл также сходится (теорема 15.2)

15.14. Подынтегральная функция и функция больше нуля на промежутке . Найдем предел частного этих функций, используя правило Лопиталя,

.

Так как интеграл сходится, то интеграл также сходится (теорема 15.3).

15.15. Подынтегральная функция и функция больше нуля на промежутке . Найдем предел частного этих функций, используя правило Лопиталя,

.

Так как интеграл расходится, то интеграл также расходится (теорема 15.3). ●

Задачи

Исследовать сходимость следующих интегралов:

15.52. . 15.53. . 15.54. .

15.55. . 15.56. . 15.57. .

Исследовать сходимость несобственных интегралов:

15.58. . 15.59. . 15.60 .

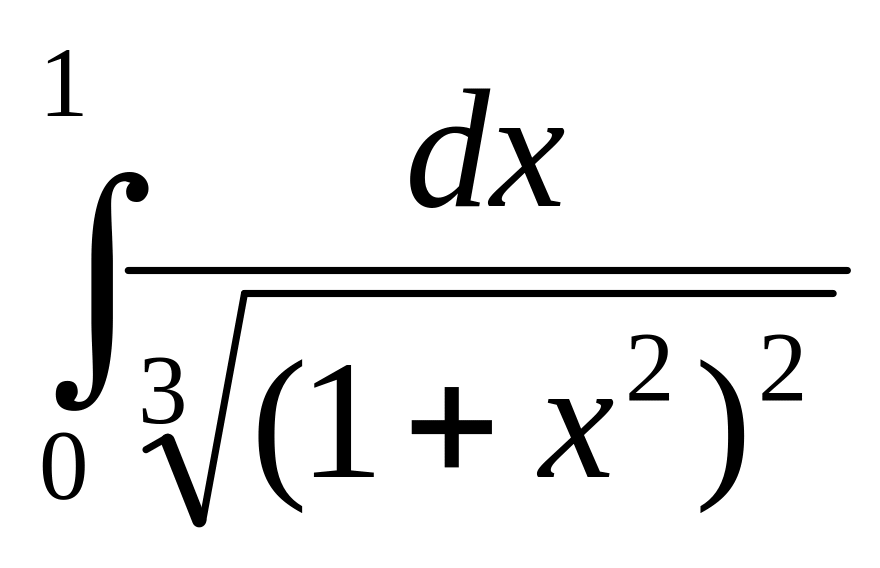15.61. . 15.62. . 15.63. .

Ответы

15.52. сходится. 15.53. расходится. 15.54. сходится. 15.55. сходится. 15.56. сходится. 15.57. сходится. 15.58. сходится. 15.59. сходится. 15.60. расходится. 15.61. сходится. 15.62. расходится. 15.63. сходится. ▲