15.4. Вычислить интеграл .
Решение
.
●
Задачи
15.1.
.
15.2.
.
15.3.
.
15.4.
.
15.5.
.
15.6.
.
15.7.
.
15.8.
.
15.9.
.
15.10.
.
15.11.
.
15.12.
.
15.13.
.
15.14. Доказать, что из сходимости
несобственного интеграла
следует, что
.
Ответы. 15.1.0,5. 15.2. Расходится. 15.3. Расходится. 15.4. 0,5. 15.5. 1.
15.6. 0,25. 15.7. 0. 15.8.
.
15.9.
.
15.10.
.
15.11.
.
15.12.
.
15.13.
.
▲
15.2 Несобственные интегралы второго рода
Определение 15.5. Пусть функция
интегрируема на промежутке
при любом достаточно малом
и не ограничена в каждой окрестности
точки
(рис. 15.2).
$$15.2 $$15.3
Несобственным интегралом от этой
функции на отрезке
называется предел
(15.1)
Если предел в правой части равенства (15.1) существует (не существует), то несобственный интеграл называется сходящимся (расходящимся).
Примеры
15.5. Доказать, что интеграл
сходится при
и расходится при
.
Решение. Если
,
то
Если же
,
то
.
●
Определение 15.6. Пусть функция
интегрируема на промежутке
при любом достаточно малом
и не ограничена в каждой окрестности
точки
(рис. 15.2). Несобственным интегралом
от этой функции на отрезке
называется предел
(15.2)
Если предел в правой части равенства (15.2) существует (не существует), то
несобственный интеграл называется сходящимся (расходящимся).
Примеры
15.6. Доказать, что интеграл
сходится при
и расходится при
.
Решение. Доказательство проводится так же, как и в примере 15.5. ●
Определение 15.7. Пусть функция
интегрируема
на любом промежутке отрезка
,
не содержащем точку
и неограничена в любой окрестности
точки
.
Несобственным интегралом от этой функции
на отрезке
называется сумма пределов
или
. (15.3)
Интеграл в левой части равенства (15.3) называется сходящимся, если сходятся оба интеграла в правой части равенства (15.3), и расходящимся, если хотя бы один интеграл в правой части этого равенства является расходящимся.
Примеры
15.7. Доказать
сходимость (расходимость) интеграла
.
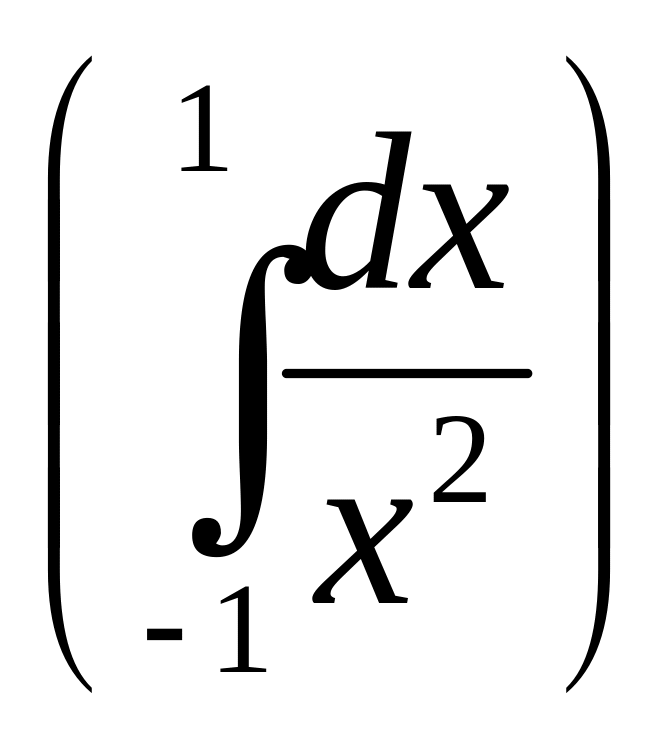Решение. Из определения следует, что
.
Так как оба интеграла в правой части
сходятся (примеры 15.5 и 15.6, где
и
соответственно), то интеграл в левой
части также сходится. Аналогично
доказывается расходимость интеграла
от функции
.●
Определение 15.8. Несобственные интегралы от неограниченных функций на отрезке называются несобственными интегралами 2-го рода.
Простейшие свойства несобственных интегралов 2-го рода
Если функция интегрируема на промежутке при любом достаточно малом и не ограничена в каждой окрестности точки , то справедливы следующие утверждения.
1. Если — первообразная функции на множестве , то справедлива формула
Доказательство. Применяя формулу Ньютона-Лейбница, имеем
.
2. Интеграл
сходится
тогда и только тогда, когда для любого
числа
сходится интеграл
,
причем справедлива формула
.
3. Если интегралы
и
сходятся, то интеграл
также сходится и справедлива формула
.
Доказательства свойств 2 и 3 аналогичны доказательствам свойств 2 и 3 для несобственных интегралов 1-го рода. ■
Аналогичные свойства справедливы и для других несобственных интегралов 2-го рода.
Задачи
Вычислить интегралы
15.15.
.
15.16.
.
15.17.
.
15.18.
.
15.19.
.
15.20.
.
15.21.
.
15.22.
.
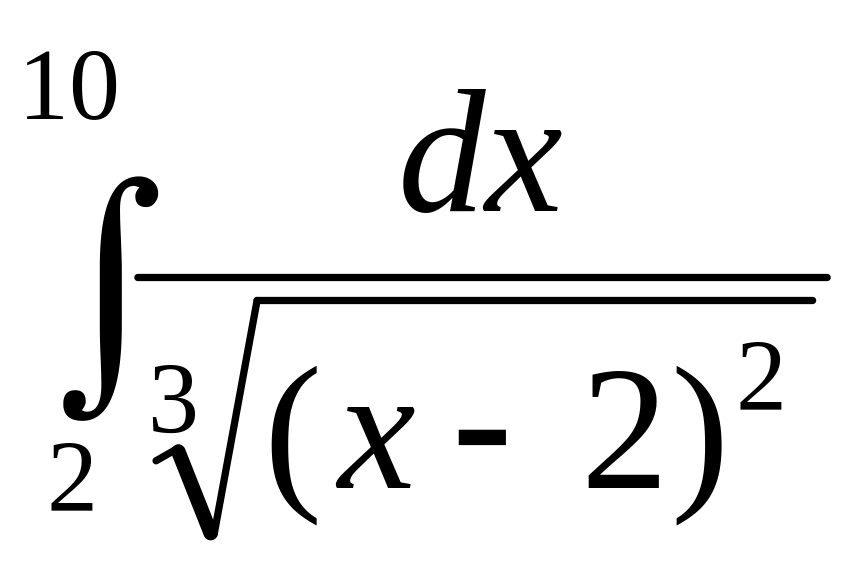15.23.
.
15.24.
.
15.25.
.
15.26.
.
15.27.
.
15.28.
.
15.29.
.
15.30.
.
15.31.
.
15.32.
.
15.33.
.
Ответы
15.15.
,
если
;
расходится, если
.
15.16. 1. 15.17.
.
15.18. расходится. 15.19.
.
15.20. 8. 15.21. расходится. 15.22. 6.
15.23..2 15.24.
.
15.25. расходится. 15.26.
.
15.27. расходится. 15.28.
.
15.29.
.
15.30.
,
если
;
расходится, если
.
15.31.
.
15.32. расходится. 15.33.
.