МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

Пясецкая Т.Е.

Индивидуальные задания по курсу «Теория вероятностей и математическая статистика»

Часть I

(Для студентов специальностей 7.080404, 7.080407, 7.091302)

Донецк, 2010

Пясецкая Т.Е.

Индивидуальные задания по курсу «Теория вероятностей и математическая статистика». Донецк, ДонНУ, 2010 г.

Настоящее пособие предназначено для организации самостоятельной работы студентов, изучающих теорию вероятностей и математическую статистику. Оно содержит тексты 16 вариантов индивидуального задания. Предлагаются решения задач одного из вариантов, приведен список рекомендуемой литературы.

Утверждено к печати Ученым Советом физического факультета Донецкого Национального Университета.

Первое индивидуальное задание охватывает следующие вопросы:

1. Классическое определение вероятности, которое связано со стохастическими экспериментами с конечным числом состояний. В этом случае все элементарные события равновозможны.

2. Геометрическое определение вероятности, которое применяется в том случае, когда пространство элементарных случайных событий, связанное с данным экспериментом, представляет собой область в евклидовом пространстве Rⁿ.

3. Теоремы сложения вероятностей для совместных и несовместных событий. Понятия зависимых и независимых событий через условные вероятности.

4. Формула полной вероятности, которую применяют в случае, когда нужно вычислить вероятность сложного случайного события. Эти события определяются при помощи полной группы событий (гипотез).

Формулы Байеса, с помощью которых можно получить переоценку вероятностей гипотез (апостериорные вероятности гипотез).

5. Схема повторных испытаний. Формула Бернулли. Предельные теоремы Муавра – Лапласа и Пуассона.

Вариант 0

1. Общество состоит из 5 мужчин и 10 женщин. Найдите вероятность того, что при случайной группировке их на 5 групп по три человека в каждой группе будет 1 мужчина.

Решение

Разбивая 15 человек на 5 троек, первую тройку можно выбрать способами, вторую, если первая уже выбрана, способами, и т.д. следовательно, всех группировок существует . Аналогично получаем, что из 10 женщин можно получить группировок по 2 в каждой . Если учесть, что в каждую группировку должен войти один мужчина, то всего благоприятствующих исходов будет

Используя классическое определение вероятности, получим

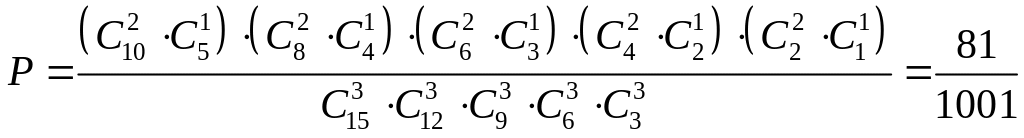
2. На отрезке АО длины L поставлены наудачу две точки В и С. Найдите вероятность того, что длина отрезка ВС окажется меньше . (Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от расположения его на числовой оси).

Решение

В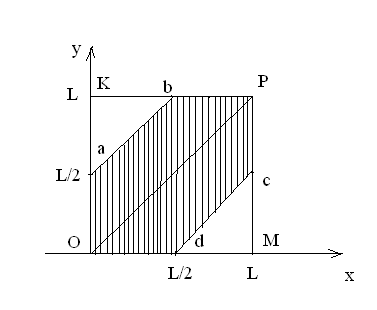 ведем в рассмотрение прямоугольную систему координат. Пусть положение точки В обозначено через х, а точки С – через у. тогда по условию . Эти неравенства удовлетворяют координаты любой точки, принадлежащей квадрату ОКРМ со стороной равной L. Совокупность этих точек образует возможные исходы эксперимента. А благоприятствующие те из них, для которых . На чертеже точки, координаты которых являются благоприятствующими, образуют заштрихованную часть квадрата

Искомая вероятность

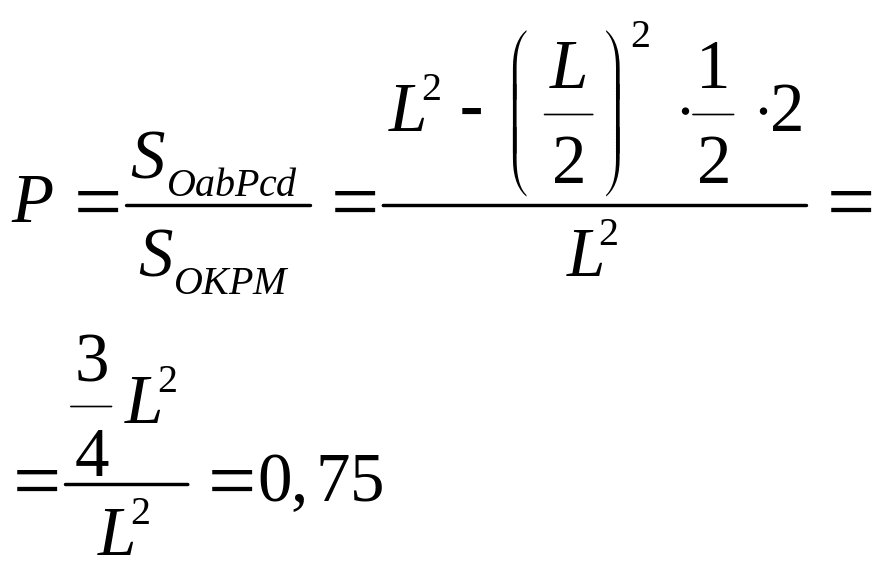
3. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,9, третий – 0,8. Найдите вероятность того, что студент сдаст а) только второй из трех; б) только один из трех; в) все три; г) по крайней мере два из трех; д) хотя бы один.

Решение

а) Введем обозначения: событие А_i – студент сдаст i-ый экзамен (i = 1, 2, 3); событие В – студент сдаст только второй экзамен. Очевидно, что , т.е. совместное наступление трех событий: студент сдаст второй экзамен и не сдаст первый и третий. Так как события - независимые, то

б) Пусть событие С – студент сдаст один экзамен из трех, т.е. сдаст только первый из трех, или только второй из трех, или только третий из трех.

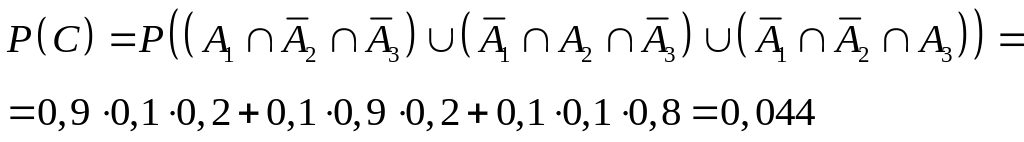
в) Пусть событие D – студент сдаст все три экзамена, т.е. . Тогда .

г)Событие Е – студент сдаст хотя бы два из трех или все три, т.е.

д) Пусть событие F – студент сдал хотя бы один экзамен, т.е. либо 1, либо 2, либо 3.

, .

Замечание. Для подсчета P(F) можно воспользоваться формулой , где означает, что студент не сдал все три предмета. . Тогда .

4. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее выпадение тройки было равно 107?

Решение

Вероятность выпадения тройки в каждом испытании , а вероятность не выпасть тройке . Наивероятнейшее число заключено в границах , где n – число испытаний. Для нашего случая

или

. Откуда

Вывод: Необходимо подбросить кость от 59 до 65 раз.

5. Учебник издан тиражом 10000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован неправильно, равна 0,0001. Найдите вероятность того, что тираж содержит 5 бракованных книг.

Решение

Непосредственный подсчет искомой вероятности по формуле Бернулли технически очень сложен.

Однако в нашем случае вероятность наступления события в каждом испытании мала, р = 0,0001, а число испытаний велико, n = 10000. В этом случае применима приближенная формула Пуассона. ( ). По таблице значений Пуассона для пары находим .

6. Вероятность того, что перфокарта набита оператором неверно, равна 0,2. Найдите вероятность того, что из 200 перфокарт правильно набитых будет а) 180; б) не меньше 180.

Решение

а) Вероятность того, что перфокарта оператором будет набита правильно равна р = 0,8. Так как n = 200 достаточно велико (условие npq = 200·0,2·0,8 = 32 > 20), то применима локальная формула Муавра – Лапласа. Найдем

( найдено по таблице)

б) Вероятность того, что из 200 перфокарт правильно набитых перфокарт будет либо 180, либо 181,…, либо 200.

Вероятность этого события можно найти по интегральной формуле Муавра – Лапласа:

, где ,

, .

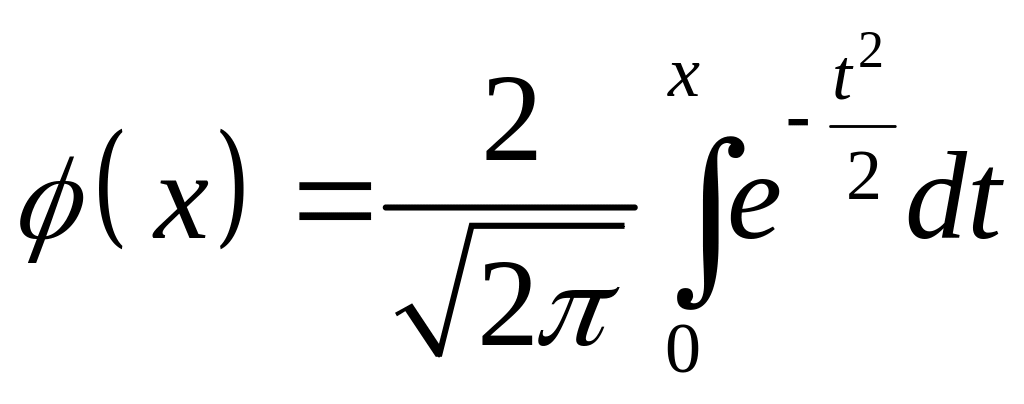Значения табулированы.

В нашем примере

.