16. Дисперсия и ско дсв. Св-ва дисперсии.
МО хар-ет СВ недостаточно полно. В кач-ве примера можно привести две СВ, к к-рых одинаковы МО и даже вероятности возможных значений, но у одной возможные значения рассеяны около ценра распределения (МО) больше, у другой – меньше.
у
9
11
р
0,5
0,5
х
-90
110
р
0,5
0,5
М(У)=1/2(9+11)=10
Для сравнения СВ по степени рассеивания около МОвводят числовую хар-ку СВ – дисперсию.
Отклонением СВ назыв-ся СВ, равное разности СВ и ее МО, т.е. отклонение СВ Х=Х-mх
Св-вом отклонения явл-ся то, что МО отклонения=0: М(Х-mх)=М(Х)-М(mх)=mх-mх=0
Дисперсией СВ Х назыв-ся МО квадрата отклонения: D(X)=Dx=M(х-mx)2
Выведем формулу более удобную для вычисления дисперсии.
D(X)=Dx=M(X-mx)2=M(Х2-2Хmx+mх2)=V(Х2)-2mxM(X)+M(mx2)=M(X2)-2mx2+mx2=М(X2)-mx2
Т.о. дисперсия=МО квадрата СВ – ее МО.
Очевидно, что дисперсия имеет размерность=квадрату размерности СВ. Поэтому вводят среднеквадратическое отклонение (СКО)=квадратному корню из дисперсии. Размерность СКО=размерности СВ: σ(Х)=σх=√Dх
Св-ва дисперсии
1. Дисперсия const=0: D(С)=0
Док-во: по опр-ю D(С)=М(С-mс)2=М(С-С)2=М(0)=0
2.Константу можно выносить за знак D, возводя ее в квадрат:D(CX)=C2D(X)
Док-во:D(CX)=M(CX-M(CX))2=M(C2(Х-М(Х))2)=М(С2)·М(Х-М(Х))2=С2·М(Х-М(Х))2=С2D(X) ЧТД
3.Дисперсия Сум мы двух независимых СВ=сумме их дисперсий:D(Х+У)=D(Х)+D(У)
Док-во:по формуле вычисления дисперсии имеем:
D(Х+У)=М(Х+У)2-М2(Х+У)=М(Х2+2ХУ+У2)-(mx+my)2=М(Х2)+2mxmу+М(У2)-mx2-2mxmy-my2=(М(Х2)- mx2)+(М(У2)-mу2)=D(X)+D(У)
Следствия:
Дисперсия суммы нес-ких взаимонезависимых СВ=сумме из дисперсий. Например для трёх: D(X+У+Z)=D(X)+D(Y)+D(Z)
2.Дисперсия суммы постоянной и СВ=дисперсии СВ: D(C+X)=D©+D(X)=0+D(X)=D(X)
Дисперсия разности двух независимых СВ=сумме их дисперсий: D(X-У)=D(X)+D(-У)=D(X)+
(-1)2D(У)=D(X)+D(У)
Пример.Реш-е: М(Х)=1/6(1+2+3+4+5+6)=7/2; М(Х2)=1/6(1+4+9+16+25+36_=91/6; Dх=М(Х2)-m2х=91/6 – 49/4=2,917; σх=√2,917=1,703
17. Биномиальное распределение. Распределение Пуассона.
Определим ДСВ как число появления случ.события в n испытаниях по схеме Бернулли, т.е. вер-ть появления события в каждом испытании постоянно и=р и исходы испытаний не зависимы друг от друга. Возможные значения СВ х1=0, х2=1,…,хn+1=n. Вер-ти этих возможных значений вычисл-ся по формуле Бернулли
Распределение этой СВ в виде табл:
х |
0 |
1 |
… |
k |
… |
n |
р |
qn |
npqn-1 |
|
|
|
pn |
Это распределение
назыв-ся биномиальным,
т.к. вер-ть возможного значения
СВ(Х)=k=общему
числу разложения бинома Ньютона
Найдем численные хар-ки биномиального распределения. Для этого рассмотрим хi – число появления события в одном i-ом испытании. Ее распределение представлено табл.
хi
0
1
р
q
р
D(Xi)=M(Xi2)-M2(Xi)=02·q+12·р-р2=р-р2=р(1-р)=pq
Т.о. МО числа появляющегося события в единичном испытании=вер-ти его появления, а дисперсия – произведению вер-ти его появления на вер-ть непоявления.
СВ Х – число появления события в n испытании=сумме СВ х1,…хn:Х=Σхi.
Пользуясь св-вами МО и дисперсии для суммы незав. СВ, имеем, что М(Х)=М(Σхi)=ΣМ(хi)=Σр=nр.
Дисперсия: D(Х)=D(Σхi)=ΣD(хi)=Σpq=npq
Т.о. mx=np; Dx=npq
Пример 1.Реш-е:
вероятнейшее число попаданий=МО.
mх=np=200·0,95=190;
СКО:
Для вычисления вер-ти появления события k раз в n испытаниях применяют формулу Бернулли. При больших n пользуются лок.теоремой Лапласа, к-рая пригодна при значениях вер-ти появления события в единичном испытании примерно удовлетворяет условию р≥1 при меньших значениях вер-ти и большом n выведем асимптотическую формулу Пуассона. Обозначим МО биномиальным распределение mx=a=np=>р=a/n. Подставим р в формулу Бернулли и преобразуем:
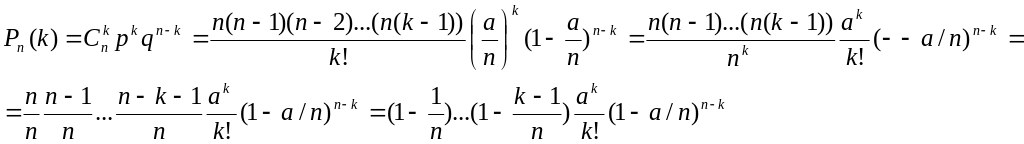
Учитывая, что n велико, найдем не саму величину Pn(k), а ее предельное значение при n→∞, к-рое дает приближенное значение Pn(k):
Т.о. для массовых, но редких событий (р мало) получаем формулу распределения Пуассона: Pn(k)≈(аk/k!)e-a.
Пример 2. n=5000; p=0.001;a=np=5.
Событие «потребитель получит не более 3 негодных деталей»=сумме несовместных событий «не повредится ни одной детали», «повредится одна», «-//- 2», «-//- 3». По т.сложения имеем, что: р(k≤3)=р(0)+р(1)+р(3)=е-5+5е-5+25/2 е-5+125/6 е-5=0,265