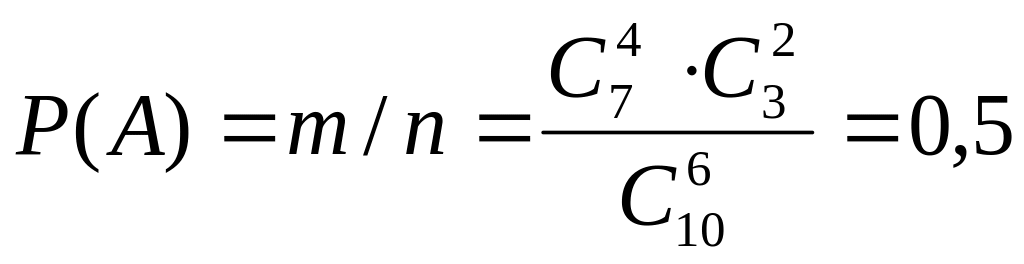2. Классическое определение в-ти. Св-ва в-ти.

Вероятность—одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют клас­сическим. Далее укажем слабые стороны этого определе­ния и приведем другие определения, позволяющие пре­одолеть недостатки классического определения.

Каждый из возможных результатов испытания назовем элементарным исходом {элементарным событием). Те элемент.исходы, в к-рых интересующее нас соб-е наступает, называется благоприятствующим этому событию.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой Р(А) = m/n

где m — число элементарных исходов, благоприятствую­щих А; n — число scex возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы не­совместны, равновозможны и образуют полную группу. Случай равновозможных соб-ий называется классич., поэтому вер-ть Р(А)=m/n . часто называют классич. Т.о. Вер-ть есть число, характеризующее степень возможности появления соб-я. Из опр-я Вер-ти вытекают ее св-ва:

1. Вероятность достоверного события равна единице.

Док-во, если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае т = п, следовательно, Р(А) = m/n=n/n=1. ЧТД

2. Вероятность невозможного события равна нулю.

Док-во, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае т — 0, следовательно, Р(А) = m/n=0/n=0. ЧТД

3. Вероятность случайного события удовлетворяет двойному неравенству0<Р(А)<1.

Док-во, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испы­тания. В этом случае 0 < m < n, значит, 0<m/n<1, следовательно,

0<Р(А)<1.

Итак, вероятность любого события удовлетворяет двой­ному неравенству 0≤Р(А)≤1

3. Основные формулы комбинаторики. Примеры непосредственного вычисления вероятностей

При непосредственном вычис­лении вероятностей часто используют формулы комбина­торики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возмож­ных перестановок

Рn=n!

где п! = 1·2·3.. ·п.

По определению, 0! = 1.

Пример 1. Написать перестановки А={a, b,c}

Р3 = 3! = 1·2·3 = 6.

(a, b, c), (a,c,b), (b,c,a), (b, a,c) (c,a,b), (c,b,a).

Размещениями называют комбинаций, составленные из п различных элементов по т элементов, которые от­личаются либо составом элементов, либо их порядком. Число всех возможных размещений

Пример 2. Сколькими способами можно рассадить 4х человек на 25 местах?

Искомое число способов=числу размещений из 25 по 4:

Сочетаниями называют комбинации, составленные из п различных элементов по т элементов, которые отли­чаются хотя бы одним элементом. Число сочетаний

Пример 3. Сколькими способами читатель может выбрать 3 книги из5?

Решен и е. Искомое число способов

Принцип умножения в комбинаторике: Пусть необходимо выполнить одно за другим каких-то k действий. Если первое действие можно выполнить n1 способами, после чего второе действие можно выполнить n2 способами, после чего 3е действие можно выполнить n3 способами и т.д. до k-го действия, к-рое можно выполнить nk способами, то все k действия вместе м.б. выполнены n1·n2·n3…nk способами.

Пример 4. Реш-е: посчитаем сначала число способов, к-рыми можно покрасить забор так, чтобы любые 2 соседние доски были окрашены в различные цвета:

1ю доску можно покрасить люб. Из трёх красок;

2ю – одной из двух оставшихся;

3ю – одной из двух оставшихся

Т.е. число способов = 3·512=1536

В полученное число вошли и способы покраски в 2 цвета. Число таких способов =6. Итого: 1536-6=1530

При решении задач комбинаторики используют сле­дующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами

Примеры непосредственного вычисления вероятностей

Пример 1. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их на­удачу. Найти вероятность того, что набраны нужные цифры.

Решение. Обозначим через В событие — набраны две нужные цифры.

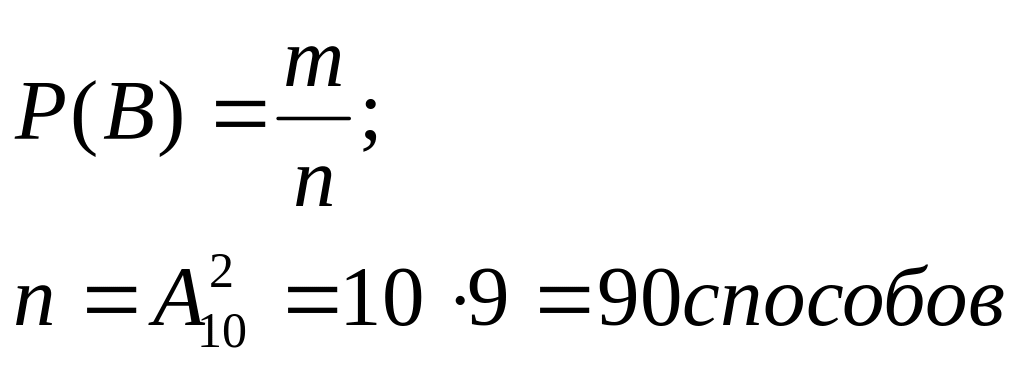
Р(В)=1/90

Пример 2. Брошены 3 монеты. Найти вер-ть того, что выпадут 2 «Г».

Реш-е: Пусть А – «выпали 2 «Г»», тогда Р(А)=m/n

n=8; m=3; Р(А)=3/8

Пример 4. В партии из 10 деталей 7 стандартных. Найти вер-ть, что среди 6 взятых наудачу деталей 4 станд.

Реш-е: А –«среди 6 взятых наудачу деталей 4 станд»