26. Генеральная совокупность и выборка. Статистическое распределение. Эмпирическая функция распределения. Полигон и гистограмма.

Изучение закономерностей массовых случайных явлений на практике осуществл.путём анализа результатов наблюдения статистических данных методами теор.вер.

Задачами мат.стат-ка явл.разработка методов получения стат.данных в результате наблюдений или эксперимента и их обработке, анализа полученных данных для практических целей.

Современную мат.стат.назв.наукой о принятии решений в усл.неопределенности.

Опр1: выб.совокупностью или выборкой называют сов-ть случайно отобранных объетов.

Опр2: генеральной сов-тью назыв совокупность объектов, из которых производится выборка.

Опр3: Объёмом совокупности (выборочной или генеральной назыв.число объектов этой совокупности).

Чтобы по данным выборки с достаточной уверенностью судить об интересующем как кол-вом признаке генер.сов-ти, т.е выборка должна быть репрезентативной. Для этого разработаны спец.способы отбора, кот.существенно зависят от особенностей изучаемых объектов.

В разл.областях техники эти способы отбора оговорены специальными руководящими документами, нормировками.

Осн.усл.репрезентативности выборки явл.случайность отбора, при кот.каждый объект должен искать одинаковую вероятность попасть в выборку.

Пусть при изучении объектов выборки наблюдались значения количественного признака х:

x₁-n₁-раз

x₂-n₂-раз

...

x_n-n_k-раз

n=Σ n_i – объём выборки

Набл.значения x_i назыв.вариантами

Последовательность вариант в возрастающем порядке назыв.вариационным рядом. Числа наблюдений n_i разл.значений количеств.признака назыв.частотами, а их отношение к объёму выборки: w_i=n_i/n –относит.частоты.

Пример 1.Реш-е: w₁=1/10; w₂=0.3; w₃=0.6

хi	2	5	7
wi	0,1	0,3	0,6

Опр4: Статистическим распределением назыв.перечень вариант и соотв.им частот или относит.частот.

При непрерывном распределении кол-венного признака статист.распределение задаётся последовательностью интервалов и соотв.им частот.

Пусть имеется стат.распредел.количеств.признака Х и х – число наблюдений при кот.наблюд.значение признака Х меньше х, n – общее число наблюдений.

Опр5: Эмпирической ф-цией распредел.назыв.ф-ция равная относит.частоте события Х<х: F*(x)=n_x/n

Т.к по теореме Бернулли относит.частота приближенно равна вероятности события, то эмпирическая ф-ция распредел.явл. примерным представлением теорет.ф-ции распределения генеральной совокупности.

Св-ва эмпирической ф-ции распредел.такие же как и у теорет.ф-ции распределения, а именно:

1. значение эмпирической ф-ции принадлежит [0;1]

2. F*(x) –неую.ф-ция

3. Если x_i наим варианта, а х_k – наиб варианта, то F*(x)=0 при х≤x_i и F*(x)=1 ghb x> x_k

Пример 2. Реш-е: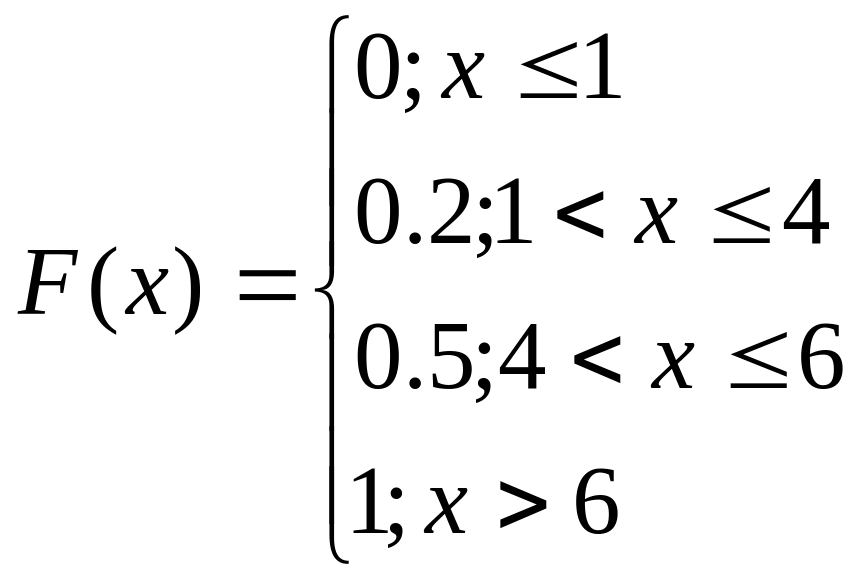

Опр6: Полигоном частот назыв.ломаная линия отрезка кот.соедин.точки (x_i;n_i)

По оси абцисс отклад.варианты x_i , а по оси ординат- соотв.им частоты. Затем соедин.точки отрезками прямых и получают полигон частот.

Опр7: Полигоном относит.частот назыв.ломаную, соедин.точки, по оси ординат откладывают относит.частоты.

При неравномерном распределении признака стоят гистограмму, для этого интервал в кот.заключены все необходимые значения признака разбивают на несколько частичных интервалов длиной h и вычисляют для каждого частичного интервала сумму частот вариант попавших в i-ый интервал.

Опр8: Гистограммой частот назыв.ступенчатую фигуру сост.из прямоугольников, основаниями которых явл.частичные интервалы длиной h, а высоты равны отношениям n_i/h

Опр9: Гистограммой относ.частот назыв.ступенчатая фигура, сост.из прямоугольников, основаниями которых явл.частичные интервалы длиной h, а высоты равны отношениям n_i/h

Гистограмма относ.частот явл.статистическим аналогом графика плотностей вероятностей теорет.распределения.

Опр10: Модой M₀ стат.распредел.назыв.варианта с наиб.частотой.

Опр11: Медианой M_е назыв.варианта для кот.значение эмпирической ф-ции распредел.ф-ции равно 0,5 f*(x_e)=0,5. x_e = M_е

Опр12: Размахом варьирования R назыв.разность м/д наиб.и наим.вариантами. R= x_max-x_min.