25. Нормальное распределение нсв. Вероятность попадания нормально распределенной св в заданный интервал.

Опр: Нормальным назыв.распределение Св с плотностью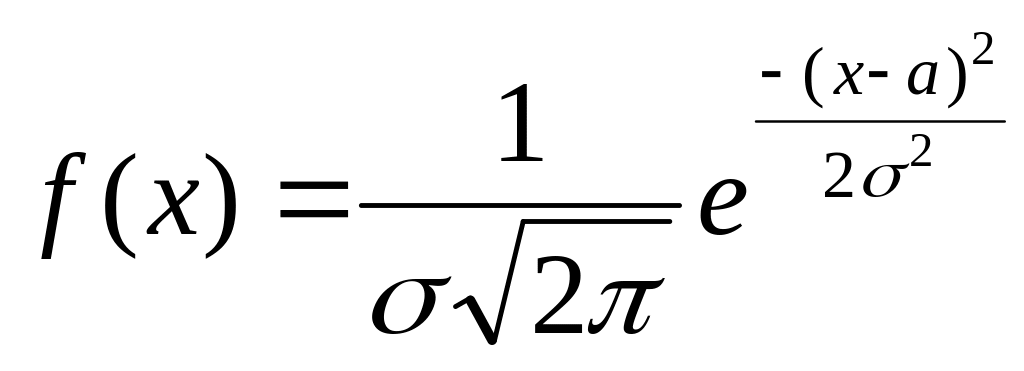 (1)

Из формулы (1) следует, что нормальное распределение определ.двумя параметрами а и σ, поэтому его обозначают N(a,σ)

Возможные значения нормального распредел.принадл.всей числовой оси ОХ. Найдем МО нормального распределения:

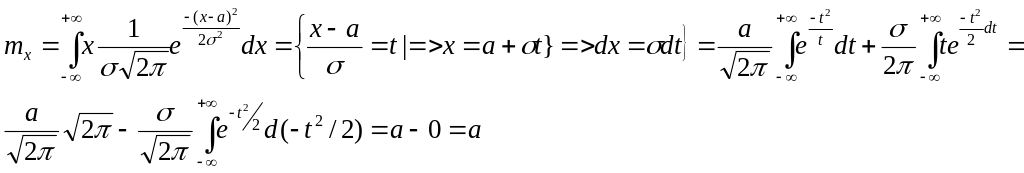
Найдём теперь дисперсию нормального распределения:

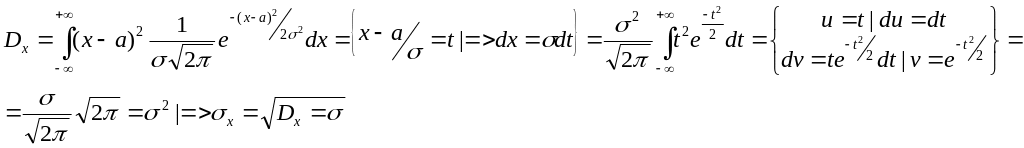
Т.О смысл параметров нормального распределения N(a,σ), то МО М(х₀)=M((x-a)/σ)= 1/σ M(x-a)=1/σ *0=0

D_x0=D((x-a)/σ)= 1/σ² D(x-a)=1/σ² *D_x=1/σ^2*σ²=1

Плотность нормированного распределения имеет вид:φ(х)=1/(√2П)*е ^–х2/2

Вероятность попадания нормально распределенной СВ в заданный интервал.

Пусть СВ Х имеет нормальное распределение N(a,σ). Найдём Р(α<x<β). Имеем, что Р(α<x<β)= Ф((β-α)/σ) - Ф((α- β)/σ)

Т.О для нормального распределения N(a,σ) имеем что Р(х(α;β))=Ф((β-α)/σ) - Ф((α- β)/σ) (1)

Рассмотрим чвстный случай когда интервал симметричен относит.МО |x-a|<ε a-ε<x<a+ε

Из формулы (1) имеем: Р(x-a|<ε)= Ф((a+ε-a)/σ) - Ф((a-ε-a)/σ)= Ф(ε/σ) - Ф(-ε/σ)=2Ф(ε/σ) (2)

Величина Х –как известно назыв.отклонением СВ от её МО, т.о формула (2) даёт способ вычислить вероятность того, что модуль отклонения СВ Х с нормальным распределением N(a,σ), не будет превышать величины ε.

Формула (1) и (2) Ф(х)- ф-ция Лапласа.

Примем в формуле (2) ε=3σ, тогда Р(x-a|<3σ)= 2Ф(3σ /σ)=2Ф(3)=0,9973

Т.е вероятность того,что модуль отклонения СВ Х от m_x=a не превышает величины равной утроенному СКО,очень близка к1

Другими словами это событие практически почти достоверно, с др.стороны вероятность противоположного события |x-a|>3σ равное P(|x-a|>3σ)=1-P(|x-a|>3σ)=1-0,9973=0,0027 – весьма мала, т.е на практике такое отклонение будет наблюдаться 0,27% случаев, что можно считать практически невозможным.

Из рассмотренного вытекает так назыв. «правило 3-х сигм». Если СВ Х распредел.нормально, то её отклонение от МО по модулю не превышает утроенного СКО.

Это правило применяется для исключения грубых ошибок при наблюдениях СВ обусловленных не закономерными случ.причинами, а грубым промахом- экспериментатора, например отчет по др. шкале приборов. Если результат наблюдения отлич.от МО по модулю больше, чем на 3σ, то его отбрасывают.

Пример. Реш-е: Х – СВ – улов рыбы за Т.

Р(Х≥20)=Р(20≤Х≤+∞)=Ф(+∞)-Ф( (20-30)/10)=0,5+Ф(1)=0,5+0,3413=0,8413

Теорема(центральная придельная теорема Ляпунова): если СВ Х явл.суммой очень большого числа взаимно незавсисимых СВ, влияние каждой из которых на всю сумму очень мало, то СВ Х имеет распределение, близкое к нормальному.

Из теоремы следует, что каждое слагаемое может иметь люб.распределение, но при выполн.усл.теоремы эта сумма слагаемых распределена приблизительно нормально.

Например, при измерении некоторой величины на результат измерения влияет множество случайных факторов (погрешность приборов, температура, давление среды и т.д.)

Каждый который вносит в результат измерения свою долю суммарной ошибки, считая, что все факторы влияют независимо др.от друга, их очень много и влияние каждого на суммарную ошибку мало, следует предположить, что суммарная ошибка распределена нормально.