20. Функция распределения вероятностей и ее свойства.

Опр1: ФР назыв.ф-ция F(x) равное вероятности того, что СВ Х примет значение меньшее х; F(x)=P(X<x)

ФР явл.аналитическим способом задания закона распределения как дискретных, так и непрерывных Св, теперь можно дать более точное определение НСВ: СВ назыв.непрерывной, если её ф-ция распредел.непрерывна и кусочно дифференцируема.

Св-ва ФР:

1)Значение ФР принадлежит отрезку (0;1); св-во следует из определения ФР. F(x)=P(X<x)

2)ФР неубывающая ф-ция: F(x2)≥F(x1), при х1>x2.

Док-во: Пусть x2>x1. Рассмотрим событие x<x1, которое явл.суммой несовместимых событий x<x1 u x1≤x≤x2, x<x2

По теореме сложения имеем, что P(x<x2)=P(x<x1)+P(x1≤x≤x2)

F(x2)=F(x1) P(x1≤x≤x2) |=> F(x2)-F(x1)= P(x1≤x≤x2)≥0 |=> F(x2)≥F(x1).

Следствие1: Вероятность того, что СВ примет значение в интервале (α;β) равна приращению ФР на этом интервале.

Следствие2: вероятность того, что НСВ примет одно определенное значение равна нулю.

3)Если возможные значения СВ принадлежат (α;β), то

1. F(x)=0 при x≤α

2. F(x)=1 при х≥β

Док-во:

1. пусть x₁≤α. Событие x<x1 невозможно, т.к по условию СВ Х значений меньше α не принимает, тогда P(x<x1)=F(x1)=0 при x1≤α

2. пуcть x2> β/ Cобытие чБч2 достоверно, т.т все возм.меньше х2. Тогда Р(x<x1)=F(x2)=1 ghb x2>β

Cледствие: Если -∞<x<∞, то имеют место предельные соотношения lim(x→∞) F(x)=0; lim(x→∞) F(x)=1

Пример. Реш-е: 1) х≤1 F(x)=0 P(-1)=P(x<-1)=0

2) -1<x<2 F(2)=0.2 P(2)=H(x<2)=0.2

2<x<3 F(x)=0.2+0.1=0.3 P(3)=P(x<3)=0.2+0.1=0.3

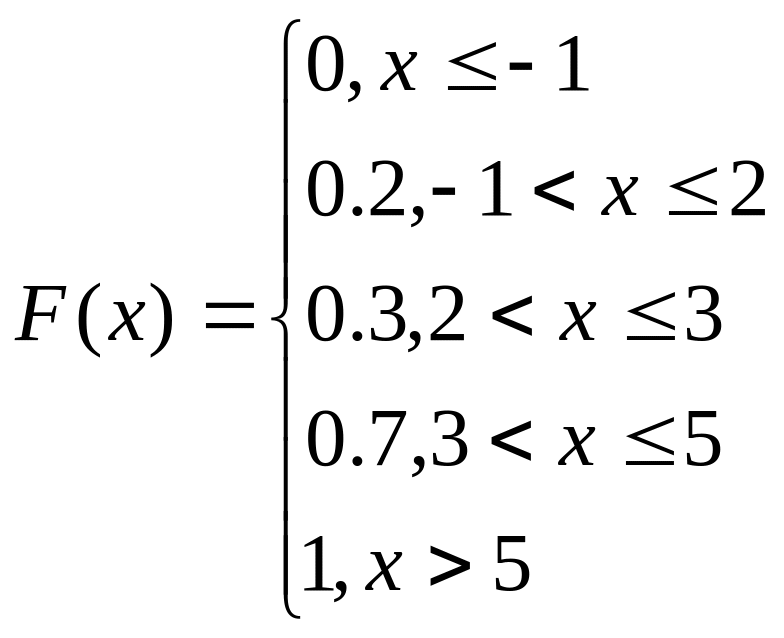
21. Плотность распределения вероятностей нсв и ее свойства.

Плотностью распределения НСВ назыв.1-ая производная ФР: f(x)=F’(x)

Согласно определению ФР явл.п/о для плотности распределения. Очевидно, что плотность распредел.непременима для описания ДСВ.

Св-ва плотности распределения:

1) Плотность распределения неотрицательна: f(x)≥0

св-во вытекает из того, что ФР неубывающая и значит её производная F’(x)=f(x)≥0

2) Вероятность попадания НСВ Х в интервал (α;β) или отрезок [α;β], где α<β равно определ.интегралу от плотности распределения на интервале (α;β):

док-во:

3) Несобственный интеграл от плотности распределения в интервале(-∞;+∞) равен 1:

Док-во: Учитывая 2), интеграл слева в формуле равен вероятности попадания СВ в интервал (-∞;+∞). Это событие очевидно достоверно, поэтому его вероятность равна 1.

Следствие: Если НСВ Х(α;β), то

22. Математическое ожидание, дисперсия и ско непрерывных св.

Пусть все возможные значения НСВ Х[a,b], разобьем отрезок на n частных отрезков внутри длиной ∆x_i. Выберем произвольно внутри каждого частного отрезка точку X_iBH и будем приближенно считать, что все возможные значения СВ Х из данного частичного отрезка сосредоточены в точке X_iBH , а вероятность того значения равна вероятности попадание СВ Х в этот частный отрезок длиной ∆x_i : P_i=P(x_i-1≤x≤x_i)=F(x_i)-F(x_i-1)=(dF(x))_i=F’(X_iBH)∆x_i=f(X_iBH)∆x_i

Взяв сумму произведений P_i X_iBH по всем частичным интервалам получим приближенно МО СВ Х, кот.мы представляли как ДСВ: М(Х)= Σ X_iBH f(X_iBH)∆x_i

Переходя к пределу при n→∞ и X_{i max}→∞ получим определ.интеграл:

(1)

Если возможные значения НСВ Х принадлежат всей оси ОХ, то интервал (1) становится несобственным: (2), при этом требуется абсолютная сходимость интеграла(2)

Дисперсией НСВ аналогично с ДСВ назыв. МО квадрата отклонения СВ Х от её МО

Если НВС Х(a,b), то дисперсия (3). Формула (3) не очень удобна для вычислений, поэтому получим др.формулу. И имеем, что:

Т.О получена след.формула для вычисл.дисперсии:

D_x=M(X)²-m²_x

Аналогично с ДСВ для НСВ определ.СКО: значению σ_х =√D_x

Все св-ва МО и дисперсии рассмотренные для ДСВ справедливы и для НСВ.