18. Простейший поток событий

Потоком событий называют последовательность со­бытий, которые наступают в случайные моменты времени. Примерами потоков служат: поступление вызовов на пункт неотложной медицинской помощи, при­бытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов эле­ментов и многие другие.

Потоки, имеющие свойства стационарности, отсутствия последействия и ординарности назыв-ся простейшими (пуассоновскими).

Свойство стационарности характеризуется тем, что вероятность появления k событий за промежуток времени t зависит только от числа k и t и не зависит от начала отсчета промежутка времени t; при этом различные промежутки времени предполагаются непере­секающимися.

Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествую­щие началу рассматриваемого промежутка, т.е. предыстория потока не сказывается на вероятности появления событий в ближайшем будущем.

Свойство ординарности характеризуется тем, что вероятность появления более одного события пренебре­жимо мала по сравнению с вероятностью появления толь­ко одного события, т.е.по­явление более одного события за малый промежуток времени практически невозможно.

Интенсивностью потока μ называют среднее число событий, которые появляются в единицу времени.

Вероятность появления k событий про­стейшего потока за время длительностью t определяется формулой Пуассона Pt(k)=(μt)k/k! (1)

Можно док-ть, что формула (1) явл-ся матем.моделью простейшего потока событий

Пример. Реш-е: Опишем интенсивность потока: μ=1/5=0,2(самолетов в минуту), тогда μt=0,2*30=6

а)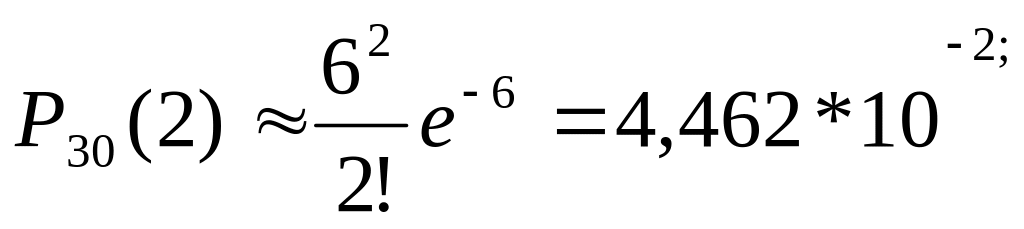 б)

в) событие k≤2 и k>2 противоположны =>

19. Закон больших чисел.

Из опр-я СВ нельзя заранее уверенно предсказать, какое возможное значение примет отдельная СВ в результате испытания (наблюдения), но если наблюдать достаточно большое число СВ, то для их суммы при выполнении некоторых условий утрачивается случ.характер и ее закономерности становятся почти достоверными. Это позволяет предвидеть ход явлений , обусловленных большим числом случ.причин. Теоремы, формулирующие условия, при к-рых это возможно, носят общее название з-на больших чисел.

Т.Чебышева: Если Х1, Х2,…,Хn попарно независимые СВ с равномерно ограниченными дисперсиями (например, не превышающими постоянного числа), то как бы ни было мало ε.>0 вер-ть неравенства |х‾-М‾(х)|< ε сколь угодно близко к1, если число СВ достаточно велико, где х‾иМ‾(х) обозн-ют ср.знач. СВ и их МО

х‾=1/nΣx_i; M‾(x)=1/nΣМ(х_i)

Др.словами, при выполнении условий т.Чебышева имеем: ,т.е. согласно т.Чебышева, если число независимых СВ достаточно велико, то почти достоверно, что отклонение средней величины СВ от средних знач.их МО будет (по абс.величине) сколь угодно малым.

Если СВ имеют одинаковые МО, к-рые обозначим а, то среднее значение МО всех СВ =а, в данном случае получим важный для практики случай ,т.е.что х‾≈а. Другими словами, при выполнении условий т.Чебышева, ср.знач. с ожидаемым МО сколь угодно мало отличается от МО, что имеет большое практич.знач. Пусть производятся измерения некоторой физ.величины. Результаты такого измерения рассматриваются как СВ х1, х2,…хn результаты такого измерения рассматриваются как СВ х1, х2,…хn, к-рые могут принимать значения, далекие истинного значения измеряемой величины, т.е. от МО, но ср.знач. всех результатов измерения будет сколь угодно мало отличаться от истинной величины, если число измерений дост.велико.

Отметим, что ↑точности путём ↑числа измерений нельзя достичь сверх некоторого предела, т.к. этому препятствует ограниченная точность приборов, применяемых при измерениях. Если прибор вносит ошибку ±α, то результаты измерений будут получены с этой же ошибкой и их ср.знач. так же будут вычислены с этой ошибкой.

Т. Бернулли

Пусть производится n независимых испытаний по схеме Бернулли. Подсчитав число появления события (m «успехов») и поделив его на число испытаний n, получим относительную частоту «успехов».

W=m/n, к-рые принимают значения, близкие к вер-ти успехов в единичном испытании. Это доказал Бернулли в своей теореме, к-рая положила начало теории вер-тей как науки.

Т.Бернулли: Если в каждом из n независимых испытаний вер-ть р появления события А постоянна, то, как бы не было мало число ε>0, вер-ть нер-ва |m/n -p|< ε сколь угодно близка к 1, т.е.: