МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

ПРИАЗОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Цветкова Е.В., Джеренова А.В.

Методические указания

к выполнению лабораторной работы № 23

«Изучение теплопроводности металлов»

(для студентов всех специальностей)

Мариуполь, 2012

УДК 531.381

Методические указания к выполнению лабораторной работы №23 «Изучение теплопроводности металлов» (для студентов всех специальностей)./ сост.Цветкова Е.В., Дже- ренова А.В.-Мариуполь:ПГТУ, 2012 – 14 с.

Содержат краткие теоретические положения по тепло-переносу в твердых телах, а также описания лабораторной установки и методики измерений.

Составитель доц. Цветкова Е.В.

ст.преп. Джеренова А.В.

Рецензент доц. Жук В.И.

Ответственный за выпуск проф. Коляда Ю.Е.

Утверждено на заседании кафедры физики протокол №6 от 13 января 2012 г.

Цель работы:

Исследовать процесс распространения теплоты вдоль металлического стержня и определить коэффициент теплопроводности металла.

Указания по подготовке к выполнению работы:

Проработайте данное руководство.

Изучите теорию по рекомендованной литературе и соответствующему лекционному материалу.

Ответьте на контрольные вопросы данного методического руководства.

1. Основные теоретические положения

Явление теплопроводности относится к явлениям переноса и заключается в способности твердых тел передавать тепловую энергию от более нагретых частей к менее нагретым. Количественно эта способность характеризуется коэффициентом теплопроводности k, который входит в уравнение теплопроводности:

,

где dQ – количество теплоты, которое переносится через площадку dS за время dt благодаря градиенту температуры .

Теплопроводность твердых тел определяется двумя составляющими: решеточной k_реш и электронной k_эл теплопроводностью

k = c₁k_реш+ c₂k_эл, (1)

где c₁ и c₂ - константы для данного материала.

Кристаллическая решетка металла состоит из положительных ионов, которые находятся в постоянном колебательном движении. Энергия колебаний этой решетки является квантовой величиной, а минимальное ее значение фононом, который рассматривается как квазичастица, так как может существовать только в веществе. Введение фонона позволяет рассматривать любое твердое тело как некую ёмкость с заключенным в ней фононным газом. Частицы этого газа движутся от стенки к стенке объёма, сталкиваются друг с другом и переносят тепловую энергию. Поэтому, решеточная составляющая коэффициента теплопроводности (1) определяется фононным газом.

Электронная составляющая соответствует переносу электронами кинетической энергии при их движении против градиента температур из области с более высокой температурой в область с более низкой температурой.

Экспериментальные данные показывают, что чистые металлы при комнатных температурах имеют теплопроводность на один-два порядка выше, чем диэлектрики. Поэтому, тепловой поток в металлах в основном переносят электроны, то есть коэффициент теплопроводности металлов определяется только электронной составляющей.

С точки зрения физического механизма явление теплопроводности представляет собой перенос энергии за счёт теплового движения частиц. Можно предполагать, что этот перенос будет тем интенсивнее, чем выше средняя скорость теплового движения частиц и средняя длина их свободного пробега . Кроме того, теплопроводность среды должна зависеть от способности системы частиц запасать тепловую энергию, то есть, от теплоёмкости этой системы.

Действительно, анализ теплопроводности идеального газа на молекулярном уровне приводит к следующему выражению для k:

. (2)

В этом выражении - теплоёмкость единицы объёма газа при постоянном объёме, которая в случае одноатомных молекул равна

, (3)

где n - концентрация молекул [м^-3], k = 1,38^.10^-23 Дж/К - постоянная Больцмана.

В металлах основную роль в процессе распространения тепла играет электронный газ – система свободных электронов, совершающих тепловое движение среди ионов кристаллической решётки. Рассмотрим классическую и квантовую модели теплопроводности металлов.

Согласно классической модели Друде – Лоренца, электронный газ можно рассматривать, как идеальный газ с тем отличием, что столкновения происходят в основном не между электронами, а между электронами и ионами кристаллической решётки. В этом случае среднюю скорость электронов можно рассчитать по формуле Максвелла

(4)

(m = 9,1^.10^-31 кг – масса электрона), а среднюю длину свободного пробега можно считать равной расстоянию между соседними ионами а.

Классическая модель, однако, приводит, по крайней мере, к двум противоречиям с экспериментом. Во-первых, расчёты по формулам (2), (3) и (4) дают заниженные значения величины коэффициента теплопроводности k. Во-вторых, в соответствии с указанными формулами, величина k пропорциональна , в то время как, согласно эксперименту, коэффициент теплопроводности металлов почти не зависит от температуры.

Квантовая модель электронного газа исходит из того, что свободные электроны распределены по энергетическим состояниям в соответствии с принципом Паули. Этот принцип не позволяет электронам в большом количестве занимать наинизшие энергетические состояния, подобно молекулам идеального газа. В результате электроны выстраиваются вверх по энергетическим уровням таким образом, что наивысший занятый уровень при Т = 0 (уровень Ферми) E_F(0) значительно превышает среднюю тепловую энергию по классической модели (например, для алюминия E_F(0) = 11,6 эВ, а средняя тепловая энергия при комнатной температуре = 0,062 эВ).

И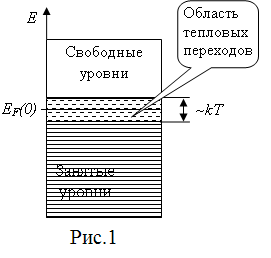 з квантовой модели вытекают важные следствия, касающиеся теплоёмкости, средней скорости и средней длины свободного пробега электронов. Во-первых, запасать тепловую энергию, то есть, энергию порядка kT может лишь сравнительно небольшая часть свободных электронов, имеющих энергию вблизи уровня Ферми (см. рис. 1). Действительно, только эти электроны имеют возможность переходить на ближайшие свободные уровни, расположенные выше E_F(0). Для электронов, находящихся значительно ниже E_F(0), такие переходы невозможны по принципу Паули, так как все ближайшие к ним уровни заняты. Относительное количество электронов с энергиями в диапазоне E_F(0)± kT равно отношению

.

В результате теплоёмкость электронного газа c_e примерно в такое же количество раз меньше теплоёмкости идеального газа (см. формулу (3)):

Более точное выражение, подученное на основе статистики Ферми-Дирака, имеет вид:

. (5)

Второе следствие из квантовой модели состоит в том, что средняя кинетическая энергия электронов воспринимающих тепловые возбуждения и, следовательно, участвующих в процессе переноса тепла, близка к . В связи с этим среднюю скорость этих электронов можно оценить из формулы

. То есть . (6)

Подставляя (5) и (6) в выражение (2) для k получаем:

. (7)

Наконец, третье следствие из квантовой модели заключается в том, что средняя длина свободного пробега электронов обратно пропорциональна температуре Т, что связано с особенностями взаимодействия электронного газа с кристаллической решёткой. Это означает (см. (7)), что в полном соответствии с экспериментом, величина k не должна зависеть от температуры. Заметим также, что величина средней длины свободного пробега по квантовой модели значительно (примерно на два порядка величины) превышает постоянную кристаллической решётки а.