3. Особливості, властиві кореляційному аналізу:

Необхідно підкреслити дві особливості, властиві кореляційному аналізу:

1) при використанні кореляційного методу вирішальне значення має всебічний, економічно усвідомлений попередній аналіз даних господарської діяльності. Слід пам'ятати, що зв'язок між ознаками і властивостями не є результатом математичних розрахунків, а лежить в природі самих економічних явищ і за допомогою методів математичної статистики можна лише виразити об'єктивно існуючі закономірності економічних процесів;

2) кореляцію можна виявити, лише досліджуючи достатньо велику сукупність спостережень, оскільки кореляційні зв'язки виявляються в формі спряженого варіювання двох або кількох зіставлених ознак.

Кореляційно - регресійний аналіз включає три етапи:

1) математико - економічне моделювання ;

2) рішення прийнятої моделі шляхом знаходження параметрів кореляційного рівняння (кореляційне рівняння, за первинною пропозицією англійського статистика - математика Ф. Гальтона, називають також рівнянням регресії);

3) оцінка і аналіз одержаних результатів.

Статистичне дослідження кореляційної залежності включає завдання визначення форми зв'язку і знаходження кількісної характеристики цієї форми. Процес встановлення форми зв'язку і вибору математичного рівняння, яке могло б найбільш повно відображати характер взаємозв'язку між ознаками досліджуваного явища, має вирішальне значення в кореляційному аналізі.

Питання вибору форми зв'язку та математичного рівняння можна вирішити на основі кількісного соціально - економічного аналізу явищ, що вивчаються, використовуючи при цьому такі методи статистичного аналізу, як графічний, статистичні групування, дисперсійний аналіз та ін.

При прямолінійному зв'язку збільшення факторної ознаки (х) викликає безперечне збільшення (чи зменшення) результативної ознаки (у) у середньому на певну величину.

Приклад. За наведеними даними зробити вирівнювання динамічного ряду по прямій:

Роки	Виробництво буд. матерiалiв, млн. т	Умовні значення років	Розрахунки
	y	t	t2	yt
2008	61	1	1	61	60,0
2009	62	2	4	124	66,3
2010	72	3	9	216	72,6
2011	80	4	16	320	78,9
2012	85	5	25	425	85,2
Підсумок

Рівняння прямої:

,

де – вирівняне (теоретичне) значення рівня ряду;

a, b – параметри;

a – постійне значення рівня ряду при t = 0;

b – швидкість зміни рівнів ряду, які визначають основну тенденцію зміни рівня ряду (виробництво цементу) у часі;

t – періоди часу або їх умовне значення.

Щоб знайти параметри рівняння прямої (a і b), застосуємо систему нормальних рівнянь:

,

де n – кількість відрізків часу; n = 5 років.

Для його вирішення зробимо необхідні розрахунки в таблиці та підставимо дані в систему нормальних рівнянь і одержимо:

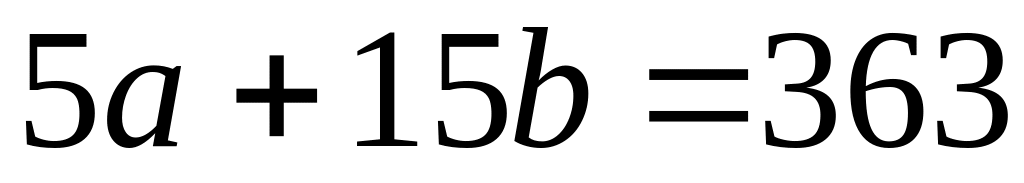
	-3
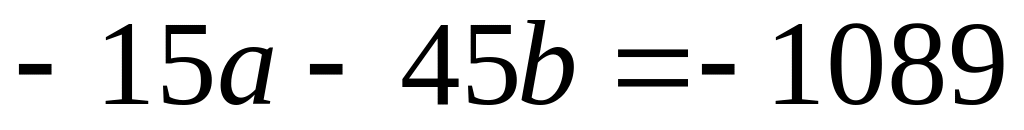
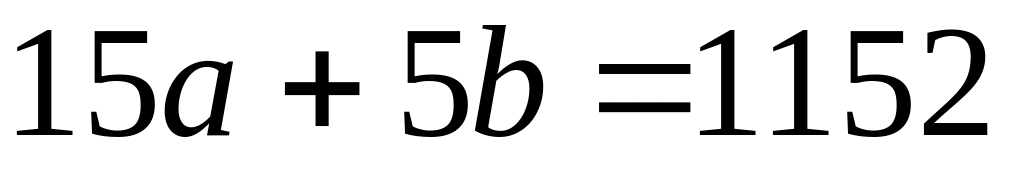
	1

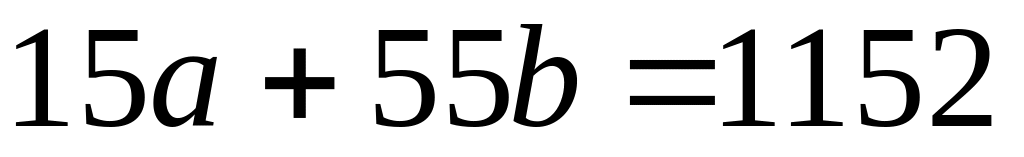
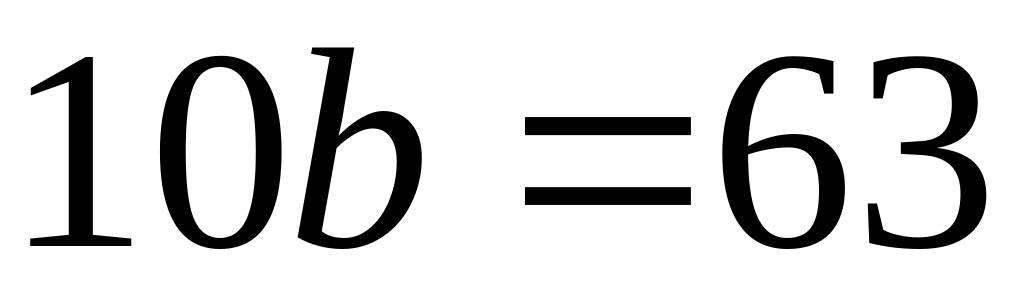
Звідси .

Підставимо 6,3 в перше рівняння, одержимо:

, звідки

.

Таким чином, визначивши параметри прямої a і b та підставивши їх в рівняння, одержимо:

.

За цим рівнянням розрахуємо теоретичні (вирівняні) значення виробництва цементу та занесемо їх до таблиці:

млн. т;

млн. т;

млн. т;

млн. т;

млн. т.

Поскільки, (емпіричні, фактичні рівні виробництва) дорівнює , то розрахунки зроблено вірно.

Рівняння може бути використано для прогнозування, тобто знаходження рівня ряду на перспективу з врахуванням виявленої тенденції виробництва за попередній період (2008 – 2012 рр.), тобто застосуємо метод екстраполяції. Наприклад, знайдемо прогнозне значення виробництва цементу на 2013 рік (t = 6);