4.3 Расчёт колонны относительно свободной оси
Определяем расстояние между ветвями колонны из условия обеспечения равноустойчивости колонны в двух плоскостях (λef = λx=58,64). Гибкость ветви для колонны с соединительными планками рекомендуется принимать в пределах λy1 = = 30...35. Принимаем λy1 = 30.
Определяем требуемое значение гибкости относительно свободной оси:
,
(82)
.
Определяем радиус инерции, соответствующий требуемой гибкости в соответствии с формулой (80):
см.
Определяем требуемое расстояние между ветвями колонны:
,
(83)
где α2 – коэффициент, зависящий от типа сечения ветвей; для сечения колонны из двух двутавров α2 = 0,60.
см.
Определяем наименьшее возможное расстояние между ветвями:
,
(84)
где bf – ширина полки профиля, принятого для ветвей колонны; для двутавра № 36:
bf = 155 мм;
100 мм – минимальный необходимый зазор в свету между полками ветвей.
мм.
Окончательно принимаем расстояние между ветвями колонны b0 = 39 см.
4.4 Проверка колонны относительно свободной оси
Определяем расчётную длину ветви колонны в соответствии с формулой:
,
(85)
где λ1 – принятая гибкость ветви, λ1 = 30;
iy1 – момент инерции двутавра № 36 относительно оси у-у, iy1 = 2,89 см.
см.
Принимаем l0=87 см.
Определяем момент инерции колонны относительно свободной оси:
,
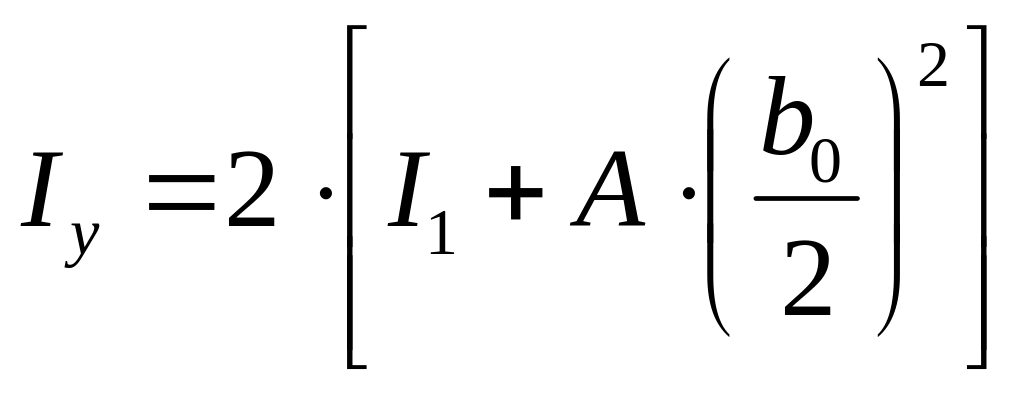(86)
где I1 – момент инерции двутавра № 36 относительно оси у-у, I1 = 516 см4;
А – площадь поперечного сечения одного двутавра № 36, А = 61,9 см2;
b0 – принятое расстояние между ветвями колонны, b0 = 39 см.
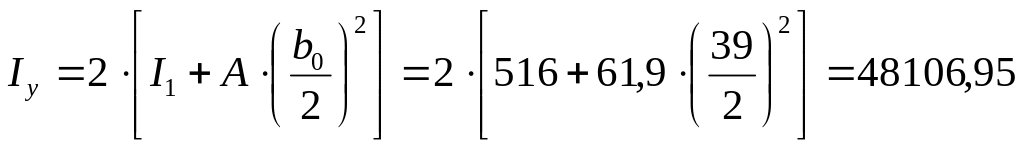см4.
Радиус инерции сечения стержня колонны относительно свободной оси определяется по формуле:
,
(87)
где Iу – момент инерции колонны относительно свободной оси, Iу = 48106,95 см4;
А – площадь поперечного сечения одного двутавра № 36, А = 61,9 см2.
Определяем гибкость колонны относительно свободной оси:
,
(88)
где lef – расчётная длина колонны, lef = 862 см;
iy – радиус инерции колонны относительно свободной оси, iy = 19,71 см.
.
Проверяем отношение погонных жесткостей ветви и планки:
,
(89)
где Is – собственный момент инерции соединительных планок, определяемый по формуле:
,
(90)
где ts – толщина соединительной планки, ts =(1/10…1/25)*hs=18,5/10=1,85 см. Принимаем ts =19 мм;
hs – высота соединительной планки, hs =(0,5…0,75)*b=0,5*39=18,5 см. Принимаем hs=19 см.
l1 – расстояние между центрами соседних соединительных планок, l1= l0+ hs=87+19=106 см;
I1 – момент инерции ветви относительно оси у-у, для двутавра № 36 I1 = 516 см4;
b0 – расстояние между осями ветвей колонны, b0 = 24,5 см.
см4.
.
При значении отношения погонных жесткостей ветви и планки более 5, приведенная гибкость колонны определяется в соответствии с формулой:
,
(91)
где λy – гибкость колонны относительно свободной оси, определённая по формуле (88); λy = 43,73;
λy1 – принятая гибкость ветви, λy1 = 30.
.
Проверяем устойчивость принятого стержня колонны в соответствии с неравенством:
,
(92)
где N – продольная сила, действующая на колонну, N = 3033,9 кН;
А – площадь поперечного сечения одной ветви колонны, А = 61,9 см2;
φу – коэффициент продольного изгиба колонны, принимаемый в зависимости от значения гибкости колонны относительно свободной оси по [8, таблица 4.5];
Для определения значения коэффициента φу воспользуемся методом интерполяции:
.
Подставляем полученное значение в формулу (91):
МПа.
МПа,
307,5 МПа < 335 МПа.
Условие выполняется, устойчивость принятого стержня колонны обеспечена.