3.3 Проверочные расчёты

3.3.1 Проверка прочности балки по нормальным и касательным напряжениям

Фактический момент инерции определяется в соответствии с формулой:

(42)

где I_w – момент инерции стенки балки, I_w = 477852,27 см⁴;

b_f – принятая ширина полки, b_f = 55 см;

t_f – принятая толщина полки, t_f = 3 см;

h_ef – расстояние между центрами полок, h_ef = 167 см.

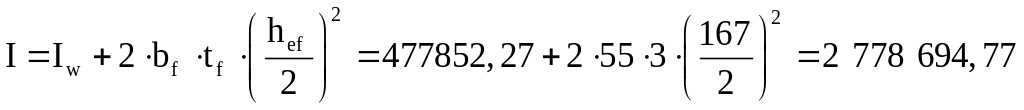см⁴.

Фактический момент сопротивления сечения определяется по формуле:

, (41)

где I – фактический момент инерции, I = 2 778 694,78 см⁴;

h_b – принятая высота главной балки, h_b = 170 см.

см³.

Прочность подобранного сечения балки на действие нормальных напряжений определяется в соответствии с неравенством:

, (42)

где М – максимальный изгибающий момент от полной расчётной нагрузки, М_mах = 10686,66 кН ·м;

W – фактический момент сопротивления сечения, W = 32690,53 см³;

R_y – расчётное сопротивление материала балки; для стали С 345 R_y = 335 МПа;

γ_с – коэффициент условий работы, γ_с = 1.

МПа,

МПа,

σ = 326,90 МПа < R_y · γ_c = 240 МПа.

Условие выполняется, прочность сечения на действие нормальных напряжений обеспечена.

Недонапряжение составляет:

Проверка прочности подобранного сечения на действие касательных:

, (43)

где Q – максимальная поперечная сила, Q = 2849,78кН;

S – статический момент полусечения, определяемый по формуле:

, (44)

где А_f – площадь поперечного сечения полки, А_f = 165 см²;

h₀ – расстояние между центрами полок, h₀ = 167 см;

А_w – площадь сечения стенки, А_w = 1,3 · 164 = 213,2 см²;

h_w – высота стенки, h_w = 164 см;

I – фактический момент инерции, I = 2 778 694,78 см⁴;

t_w – принятая толщина стенки, t_w = 1,3 см;

R_s – расчётное сопротивление стали сдвигу, R_s = 195,22 МПа

γ_с – коэффициент условий работы, γ_с = 1.

Подставляем необходимые значения в соответствующие формулы:

см³.

МПа,

МПа,

τ = 146,737 МПа < R_s ·γ_c = 195,22 МПа.

Условие выполняется, прочность сечения на действие касательных напряжений обеспечена.

3.2.3 Проверка жёсткости главной балки

Относительный прогиб главной балки определяется по формуле:

, (45)

где q_n – нормативная погонная нагрузка на балку, q_n = 318,44 кН/м;

l₁ – пролёт главной балки, l₁ = 15 м;

Е – модуль упругости прокатной стали, Е = 2,06 · 10⁵ МПа;

I_x – момент инерции главной балки относительно оси х, I_x = 2 778 694,78 см⁴.

.

Сравниваем полученное значение с предельным прогибом балки f_u (аналогично формуле (17)):

,

.

Условие выполняется, жёсткость главной балки обеспечена.

3.3.3. Проверка общей и местной устойчивости главной балки

Проверка общей устойчивости главной балки не требуется, так как на балку передаётся статическая равномерно распределённая нагрузка от жёсткого настила, опёртого на верхний пояс балки и жёстко с ним связанного.

Проверка местной устойчивости стенки выполняется с учётом значения условной предельной гибкости и наличия местной нагрузки на пояс балки.

Определяем значение условной гибкости λ_w:

, (46)

где h_w – высота стенки, h_w = 164 см;

t_w – принятая толщина стенки, t_w = 1,3 см;

R_y – расчётное сопротивление материала балки; для стали С 345 R_y=335 МПа;

Е – модуль упругости прокатной стали, Е = 2,06 · 10⁵ МПа;

.

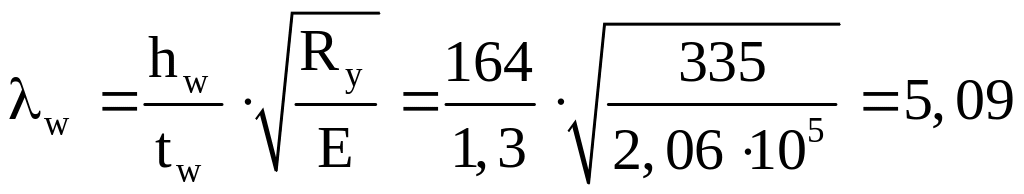Условная гибкость λ_w > 3,2, следовательно, стенку нужно укреплять поперечными ребрами жесткости

Требуемая ширина выступающей части ребра (для стенки, укреплённой только поперечными симметричными парными рёбрами жёсткости) определяется в соответствии с формулой:

, (47)

где h_ef – расстояние между центрами полок, h_ef = 167см = 1670 мм.

мм.

Принимаем ширину выступающей части ребра жёсткости b_h = 100 мм.

Требуемая толщина ребра жёсткости определяется по формуле:

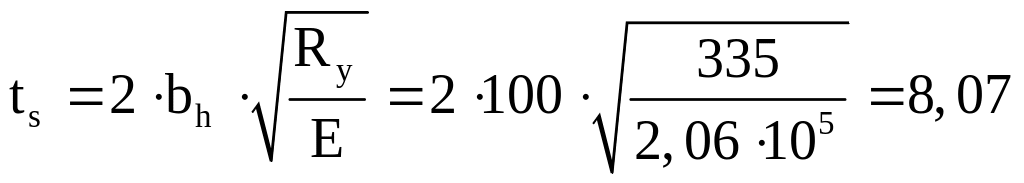мм.

В соответствии с сортаментом листовой стали, принимаем толщину ребра жёсткости

t_s = 10 мм.

Определяем протяжённость зоны учёта пластических деформаций, в пределах которой необходима установка рёбер жёсткости под каждой балкой настила:

, (48)

где l₁ – пролёт главной балки, l₁ = 15 м;

h_b – принятая высота главной балки, h_b = 170 см;

h_w – высота стенки, h_w = 164 см;

с₁ – коэффициент, учитывающий развитие пластических деформаций при одновременном действии изгибающего момента М и поперечной силы Q, с=1,1.

Подставляем полученное значение в формулу (48):

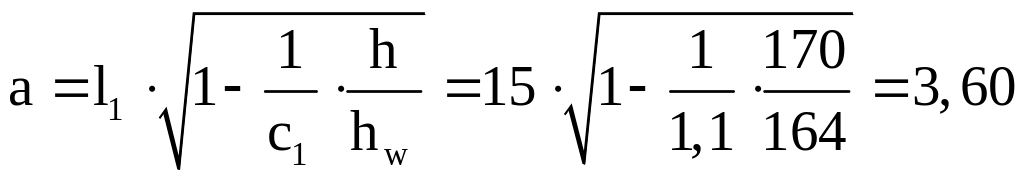м.