6. Энергетическая зависимость сечений взаимодействия для типичных материалов, используемых в ядерных реакторах. Особенности сечений для нуклидов ядерного топлива.

Рождающиеся при делении ядер нейтроны имеют энергию в диапазоне 0.1 – 10 Мэв Ē=2 Мэв. В последующем при неупругом и упругом рассеянии нейтроны снижают кинетическую энергию вплоть до энергии теплового движения ядер среды. Характер взаимодействия нейтронов с ядрами различен в диапазоне энергии от 0 – 10 Мэв.

Поэтому обычно весь диапазон энергий нейтронов в ядерном реакторе разбивают на три области:

область быстрых нейтронов…………….. 0.1 – 10 Мэв;(спектр деления)

область промежуточных нейтронов …….0.2 – 10⁵ эв;

область тепловых нейтронов……………. 0 – 0.2 эв.

Быстрые нейтроны.

Полное сечение в этой области примерно равно где R – радиус ядра,  - длина волны нейтрона с энергией Е.

1. Главная особенность этой области состоит в том, что полное сечение есть сечение рассеяния σ_s=σ_n + σ_n’. Пороги неупругого рассеяния лежат как раз в этой области.

σ_ - очень маленькое и P_f = = близко к единице.

2. В этой области не равны нулю сечения деления четно-четных ядер.

Промежуточные нейтроны.

Резонансные явления составляют наиболее характерную особенность промежуточной области энергий, в связи, с чем ее также называют резонансной.

Резонансы в зависимости сечений от энергий свойственны в той или иной мере подавляющему числу ядер и расположены практически во всем интервале энергий реакторных нейтронов. Однако на физику реактора существенно влияет резонансная структура лишь в зависимости от энергий сечений деления и радиационного захвата для тяжелых ядер. Резонансы для этих ядер занимают область Е ~ 1 ÷ 10³ эв.

Что можно сказать в общем случае

а) const для всей области энергий.

б) много меньше в области Е~1кэв и велики в области Е~0-1эв.

в) для быстрых нейтронов

для медленных нейтронов.

г) наряду с законом есть область резонансов , очень большое.

Энергетическая зависимость сечения

7. Замедление нейтронов. Непрерывная и дискретная модели описания процесса замедления.

8. Перенос нейтронов. Диффузия как непрерывная модель переноса нейтронов.

Рассмотрим баланс нейтронов в элементарном пространственном объеме ΔV с поверхностью ΔS, расположенным около точки .Баланс нейтронов отражает закон сохранения нейтронов в объеме, т.е. тот факт, что разность между скоростью генерации нейтронов в объеме и скоростью исчезновения нейтронов из объема есть скорость изменения числа нейтронов в объеме.

В результате получим уравнение:

Первый член этого уравнения описывает разность между скоростью утечки через границу объема и скоростью «втечки» нейтронов через туже границу, второй – скорость поглощения нейтронов в единице объема, третий – скорость появления нейтронов в результате деления ядер среды в единичном объеме, четвертый – скорость генерации нейтронов внешним (заданным) источником в единичном объеме.

Для расчета скорости реакции i-го типа взаимодействия нейтронов с ядрами среды в фазовом объеме необходимо соответствующее типу реакции макроскопическое сечение умножить на плотность потока нейтронов и на величину фазового объема. С учетом этой зависимости скорость реакций поглощения нейтронов и генерации нейтронов определяются выражениями:

Если задана функция распределения мощности внешних источников нейтронов - , то скорость генерации нейтронов в фазовом объеме внешними источниками записывается как .

Член утечки можно записать следующим образом, если в ходе математических преобразований использовать теорему Остроградского-Гаусса и принять во внимание, что рассматриваемый объем – элементарный:

.

Плотность потока нейтронов есть произведение плотности нейтронов на объем.

Учитывая все выше полученные выражения и подставляя их в общее уравнение, сократим на ΔV, получим уравнение баланса скоростей процессов в единичном фазовом объеме:

Уравнение получено в рамках следующих предположений:

• Все функции – статистические величины;

• Нейтрон рассматривается как точечная частица;

• Взаимодействия нейтрон-нейтрон не учитываются;

• Нейтрон – стабильная частица;

• Все нейтроны имеют одну и ту же энергию.

Используем закон Фика. Закон Фика – уравнение, которое в рамках дополнительных предположений устанавливает связь между плотностью потока нейтронов и вектором тока нейтронов. Дополнительные предположения состоят в том, что рассматриваем перенос нейтронов в большой, слабо поглощающей среде, состоящей из тяжелых ядер, далеко (более 2-х, 3-х длин свободного пробега) от локальных неоднородностей (внешние локализованные источники, граница между двумя средами, граница среда-вакуум).

Подставляя это выражение в уравнение баланса скоростей, получим уравнение диффузии для моноэнергетических нейтронов:

9. Основные процессы, влияющие на баланс нейтронов в размножающих средах. Коэффициент размножения бесконечной размножающей среды и его составляющие. Потенциальная возможность осуществления самоподдерживающейся реакции деления.

Рассмотрим простейшую физическую модель: имеется бесконечная однородная размножающая среда, состоящая из смеси горючего (например U-235), порогового нуклида (U-238), замедлителя и поглотителя. Процесс размножения нейтронов в бесконечной мультиплицирующей среде можно оценить количественно, если проследить за судьбой вторичных нейтронов, рождающихся в результате деления горючего. В процессе деления рождаются нейтроны, энергия которых может быть как больше, так и меньше порога деления U-238. Нейтроны с энергией Е_н  Е_пор могут вызывать деление ядер U-238. Таким образом, число нейтронов в единице объёма с энергией Е_н  Е_пор , будет больше числа первоначально родившихся нейтронов деления за счёт деления U-238. Это увеличение числа замедлившихся нейтронов в результате размножения на быстрых нейтронах характеризуется коэффициентом , равным числу быстрых нейтронов, которые замедлились до энергии ниже порога деления U-238, отнесённому к одному быстрому нейтрону, появившемуся при делении U-235 тепловыми нейтронами. Если предположить, что в начальный момент времени в мультиплицирующей среде число нейтронов от деления U-235 есть n₀, то за счёт деления U-238 быстрыми нейтронами оно возрастёт до значения n₀. Эти нейтроны, сталкиваясь с ядрами среды, замедляются до энергии ниже порога деления U-238.

В процессе замедления часть нейтронов претерпевает радиационный захват ядрами U-238 не достигнув тепловой энергии. Радиационный захват нейтронов характеризуется коэффициентом  - вероятность того, что быстрый нейтрон в процессе замедления избежит радиационного захвата. Захват надтепловых нейтронов при замедлении носит специфический характер. В этой области энергий сечения захвата ядер со средними и большими массовыми числами имеет ярко выраженную резонансную структуру. Поэтому коэффициент  ещё называют вероятностью избежать резонансного захвата. Захват на лёгких ядрах замедлителя в этой области энергий ничтожно мал и в формировании  не играет никакой роли.

Таким образом, до тепловой энергии замедляются n₀ нейтронов. Но даже тогда, когда нейтроны стали тепловыми, не все они поглотятся в уране. Часть их будет захвачена ядрами замедлителя. Если ввести коэффициент , определив его как вероятность захвата теплового нейтрона делящимся веществом, (его называют коэффициентом использования тепловых нейтронов), то ядрами горючего (U-235) будет захвачено n₀ нейтронов.

При захвате нейтрона ядром U-235 не все они будут делиться, часть реакций будут идти по каналу радиационного захвата. Поэтому вводится коэффициент - среднее число нейтронов деления на один захваченный тепловой нейтрон в U-235. Очевидно, что , где - среднее число нейтронов деления.

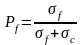- вероятность реакции деления при захвате U-235 теплового нейтрона.

Таким образом, если пренебречь делением U-235 на замедляющихся нейтронах, то во втором поколении число быстрых нейтронов деления возрастёт до значения .

Отношение числа нейтронов второго поколения к числу нейтронов первого поколения называют коэффициентом размножения в бесконечной однородной среде или просто .

= / = .

Это выражение называется формулой четырёх сомножителей для . Подчеркнём ещё раз, что формула четырёх сомножителей описывает размножение нейтронов в сильно замедляющей среде, когда основная доля процессов деления приходится на тепловые нейтроны. Следовательно, она служит для описания размножения нейтронов в реакторе на тепловых нейтронах.

Таким образом при =1 возможно самоподдерживающаяся реакция деления, т.е. число нейтронов второго поколения будет равно числу нейтронов первого поколения.

10. Демонстрация возможности создания критического реактора на примере одномерной модели с одной группой нейтронов. Понятие материального и геометрического параметров. Эффективный коэффициент размножения и условие критичности.

Рассмотрим стационарное уравнение диффузии для моноэнергетических нейтронов в условиях применимости закона Фика (большая, слабопоглощающая среда, состоящая из тяжелых ядер, далеко (более 2х-3х длин свободного пробега) от локальных неоднородностей (локаллизованые источники, граница раздела двух сред, граница среда-вакуум)):

Введем условие равенства нулю потока на экстраполированной границе среды:

Поделим уравнение на коэффициент диффузии и произведем замену:

,

Где - коэффициент размножения нейтронов в бесконечной среде,

- квадрат длины диффузии,

- материальный параметр среды, зависящий только от свойств мультиплицирующей среды.

Итак, общая постановка задачи в одногрупповой теории такова: требуется найти ограниченное положительное решение уравнения

с граничными условиями

С математической точки зрения сформулированная выше задача является задачей на определение собственных чисел и собственных функций оператора Лапласа

Как правило, это задача имеет счетное множество линейно независимых решений , причем каждой собственной функции соответствует собственное число , причем для этих чисел имеет место следующее соотношение

Наименьшему собственному значению соответствует знакопостоянная собственная функция , а все остальные собственные функции являются знакопеременными в области изменения координат внутри активной зоны.

Следовательно, поставленная стационарная задача имеет решение только в том случае, когда 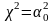, причем функция распределение потока нейтронов имеет вид

где C – произвольное положительное число. Наименьшее по абсолютной величине собственное число задачи называют геометрическим параметром, поскольку он зависит только от размеров и формы активной зоны, но не зависти от свойств мультиплицирующей среды. Равенство означает, что для заданной формы тела существуют такие размеры, при которых в ограниченной размножающей среде возможен стационарный процесс деления ядер. Соответствующие размеры такой среды называются критическими размерами, а отвечающим этим размерам объем мультиплицирующей среды – критическим объемом. Масса делящегося вещества в такой среде называется критической массой.

По определению эффективным коэффициентом размножения называется такое число, на которое надо разделить источник нейтронов деления, чтобы реактор стал критическим.

Производя обычные преобразования, приведем уравнение к виду:

Это уравнение называется уравнением условно критического реактора. Если реактор был критическим, то . Следовательно, эта величина подобна коэффициенту размножения бесконечной среды. Условие критичности реактора позволяет выразить эффективный коэффициент размножения через нейтронно-физические характеристики размножающей среды и геометрический параметр активной зоны, а именно:

Найдем критические размеры размножающей среды для различных геометрических форм активной зоны, граничащей с вакуумом.

Активная зона реактора в форме шара.

В сферически симметричном случае лапласиан имеет вид

и волновое уравнение

Сделаем подстановку , в результате которой получим следующее уравнение относительно функции f

Общее решение этого уравнения

Поскольку - ограниченная функция, то С₂=0 и

Воспользуемся граничным условием

Из условия критичности видно, что реактор может находиться в стационарном состоянии при определенном значении R (всюду в дальнейшем мы опустим нижний индекс у экстраполированного размера активной зоны).

Этот радиус и является критическим радиусом для сферической активной зоны.

Общее решение имеет произвольную постоянную С, которая характеризует мощность реактора. Произвольность константы отражает тот факт, что критический реактор может иметь произвольную мощность.

Реактор в форме цилиндра конечной высоты.

Рассматривается цилиндрическая активная зона радиуса R и высотой H. Учитывая вид лапласиана в цилиндрической геометрии, получим следующее уравнение на собственные значения

Решение этого уравнения в частных производных будем искать методом разделения переменных, представив решение в виде . После подстановки предполагаемого решения в исходное уравнение, получим

Представляя геометрический параметр в виде суммы двух чисел исходное уравнение можно представить в виде системы двух обычных дифференциальных уравнений с соответствующими краевыми условиями

Общее решение первого уравнения системы

где функция Бесселя нулевого индекса, N₀ – функция Неймана нулевого индекса, которая имеет логарифмическую особенность при r=0 и поэтому в силу ограниченности потока нейтронов необходимо положить С₂=0, так что решение будет