
Особые ситуации симплекс-метода.
1) Опорный
план найден, есть отрицательный элемент
в целевой строке (например, в столбце с
номером
 ),
но нельзя выбрать разрешающий элемент
в
-м
столбце.
),
но нельзя выбрать разрешающий элемент
в
-м
столбце.
Вывод: максимум функции равен .
2) Опорного плана нет, а при решении вспомогательной задачи максимальное значение функции w строго меньше нуля.
Вывод: исходная система уравнений несовместна.
3) Опорный план есть, он не оптимален и в свободном столбце имеется один или несколько нулей (то есть при выборе разрешающей строки минимальное отношение элементов свободного и разрешающего столбца равно 0).
Вывод: мы находимся в вершине, где пересекается больше плоскостей, чем размерность задачи.
Правило выбора разрешающего элемента такое: Если элемент разрешающий строки, который находится напротив нулевого элемента свободного столбца положителен, то его надо взять в качестве разрешающего, а если отрицателен, то следует выбрать тот, для которого достигается минимум среди всех остальных неотрицательных соотношений.
Пример.
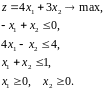
Записываем в виде уравнений:
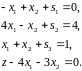
Записываем в виде симплекс-таблицы:
-
Б
1
1
1
0
0
0
1
0
1
0
4

1
1
0
0
1
1
4
3
0
0
0
0
1-я итерация жорданова преобразования.
-
Б
0
3/4
1
1/4
0
1
1
1/4
0
1/4
0
1
0
0
1/4
1
0
0
0
4
0
1
0
4
2-я итерация жорданова преобразования.
-
Б
0
0
1
2/5
0
1
1
0
0
1/5
1/5
1
0
1
0
1/5
4/5
0
0
0
0
1/5
16/5
4
Графическая иллюстрация
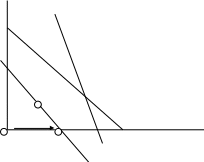
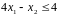


1
1
