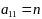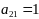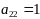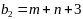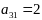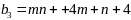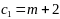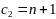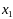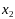Вариант задания выбирается в соответствии с двумя последними цифрами шифра A и B. Каждая задача зависит от двух числовых параметров m и n, которые определяются по цифрам A и B из таблиц:
-
A
0
1
2
3
4
5
6
7
8
9
m
2
6
4
8
8
2
6
4
4
6
-
B
0
1
2
3
4
5
6
7
8
9
n
3
5
1
7
9
1
3
7
5
9
Например, студент с шифром 12-34 (A=3, B=4) решает задачи со значениями m=8, n=9.
На собеседовании по каждой контрольной работе проверяется самостоятельность выполнения студентом контрольной работы и его готовность к сдаче зачета или экзамена.
Задача оптимального производства продукции
Предприятие
планирует выпуск двух видов продукции
I и II, на производство которых расходуется
три вида сырья A, B, и C. Потребность
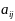 на каждую единицу
на каждую единицу
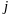 -го
вида продукции
-го
вида продукции
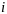 -го
вида сырья, запас
-го
вида сырья, запас
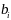 соответствующего сырья и прибыль
соответствующего сырья и прибыль
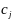 от реализации единицы
-го
вида продукции задана таблицей:
от реализации единицы
-го
вида продукции задана таблицей:
Виды сырья |
Виды продукции |
Запасы сырья |
||
I |
II |
|||
A |
|
|
|
|
B |
|
|
|
|
C |
|
|
|
|
Прибыль |
|
|
|
|
План (ед) |
|
|
|
|
Для производства
двух видов продукции I и II с планом
и
единиц составит целевую функцию прибыли
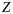 и соответствующую систему ограничений
по запасам сырья, предполагая, что
требуется изготовить в сумме не менее
и соответствующую систему ограничений
по запасам сырья, предполагая, что
требуется изготовить в сумме не менее
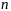 единиц обоих видов продукции.
единиц обоих видов продукции.
Составить оптимальный
план
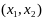 производства продукции. обеспечивающий
максимальную прибыль
производства продукции. обеспечивающий
максимальную прибыль
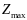 .
Определить остатки каждого вида сырья.
Задачу решить симплекс-методом.
.
Определить остатки каждого вида сырья.
Задачу решить симплекс-методом.
Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль .
Произвести анализ модели на чувствительность. Найти двойственную цену дефицитных видов сырья, максимальное значение закупок дефицитных видов сырья, которое приносит прибыль при сохранении статуса сырья, а также границы изменения цены на товар, при которых найденный план остается оптимальным.
Линейное программирование.
Задача. Фирма изготавливает два вида красок для внутренних (В) и наружных (Н) работ. Используется два расходных продукта А и С, суточные запасы которых ограничены (не более 6 т для продукта А и не более 8 т для С). Расходы продуктов А и С на 1 т красок .
-
В
Н
А
1
2
С
2
1
Суточный спрос на В не превышает спроса на Н более чем на 1 т. Спрос на краску В не превышает 2 т. Оптовые цены: 3 тыс. $ за 1 т краски Н и 2 тыс. $ за 1 т краски В.
Какое количество краски каждого вида должна производить фабрика, чтобы доход от продажи был максимальным?
Решение.
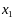 и
- суточный объем производства краски Н
и В.
и
- суточный объем производства краски Н
и В.
Целевая
функция
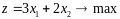 .
.
Ограничения:
на расход исходных продуктов
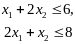
на
величину спроса

Объем
производства не может быть отрицательной
величиной
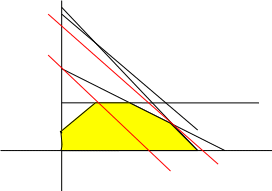
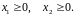 Построим многоугольник, координаты
точек которого удовлетворяют всем
ограничениям.
Построим многоугольник, координаты
точек которого удовлетворяют всем
ограничениям.
 8
8
3
2
1
2 4 6
Найдем пересечения прямых, являющихся границами соответствующих полуплоскостей.
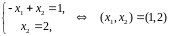
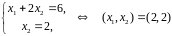
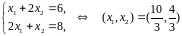
Множество
допустимых точек – шестиугольник с
вершинами (0,0), (0,1),
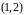 ,
,
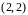 ,
,
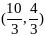 ,
(4,0). Максимум
,
(4,0). Максимум
 достигается в точке
и равен
достигается в точке
и равен
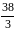 .
.
Симплекс-метод решения задачи линейного программирования.
Постановка задачи.
Задача с ограничениями типа равенства
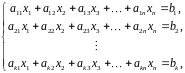

Функционал
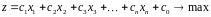
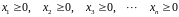
Приведение ограничений к стандартной форме.
1. Неравенства сводятся к равенствам.

Вводим остаточную
переменную
 .
.
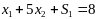
Если ограничение интерпретируется как расход ресурса, то - это остаток, неиспользуемая часть.
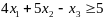
Вводим избыточную
переменную
 .
.

2. Правая часть ограничений должна быть положительной.
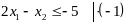
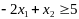
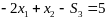
В симплекс-методе реализуется упорядоченный процесс, при котором, начиная с некоторой исходной угловой точки, осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.
Решение, соответствующее начальной точке алгоритма, называется начальным (опорным) решением.
Частный случай:
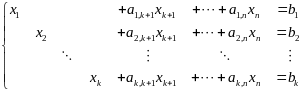

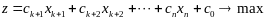
Решение
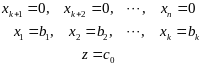
Переменная

базисная,
если она входит только в одно уравнение
системы ограничений (с коэффициентом
1) и не входит в функцию
базисная,
если она входит только в одно уравнение
системы ограничений (с коэффициентом
1) и не входит в функцию
 .
.
Небазисные переменные называются свободными.
Если в
системе ограничений имеется ровно
 базисных переменных, то скажем, что
получен опорный план. Опорный
план
это точка допустимого множества, для
которой базисные переменные равны
элементам свободного столбца, а свободные
переменные равны нулю.
базисных переменных, то скажем, что
получен опорный план. Опорный
план
это точка допустимого множества, для
которой базисные переменные равны
элементам свободного столбца, а свободные
переменные равны нулю.
Критерий оптимальности.
Все коэффициенты при свободных переменных в функции отрицательны.
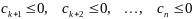
Улучшение опорного плана.
Пусть
для опорного плана имеем:
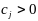 для какой-либо свободной переменной
для какой-либо свободной переменной
 .
.
Утверждение.
Можно
увеличить значение функции
,
если перейти к новому опорному плану,
который получается при помощи полного
жорданового исключения с разрешающим
столбцом
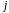 и разрешающей строкой, которая выбирается
по следующему правилу.
и разрешающей строкой, которая выбирается
по следующему правилу.
Составим
отношения
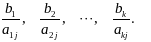
Тогда разрешающая строка – та, в которой достигается минимум из тех отношений, которые являются положительными.
Если
все отношения отрицательны, то максимум
функции
равен
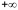 .
.
Доказательство.
1) Данное жорданово преобразование сохраняет число базисных переменных и оставляет положительными элементы свободного столбца.
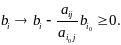
2) Функция возрастает:

Смежные экстремальные точки отличаются одной переменной. При каждой итерации симплекс – метода осуществляется переход из одной экстремальной точки в другую (смежную) точку.
Симплекс – алгоритм.
1. Определить начальное допустимое базисное решение.
2. Из числа не базисных элементов выбирается та, увеличение которой улучшит значение целевой функции. Если такой переменной нет, решение оптимально.
3. Из числа переменных текущего базиса выбирается исключаемая переменная.
4. Находится новое базисное решение.
ПРИМЕР.
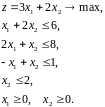
Записываем в виде уравнений:
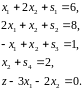
Модель содержит 4 уравнения и 6 неизвестных в каждой экстремальной точке 2 переменные равны 0.
Записываем в виде симплекс-таблицы:
-
Б
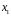
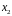
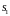
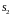
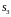
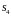
1
1
2
1
0
0
0
6
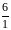
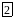
1
0
1
0
0
8
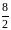
1
1
0
0
1
0
1
0
1
0
0
0
1
2
3
2
0
0
0
0
0
Обе
небазисные переменные
и
в строке для целевой функции имеют
отрицательные коэффициенты. Это
эквивалентно положительным коэффициентам
в исходной целевой функции. Следовательно,
план не оптимален, и
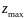 можно получить, увеличивая
или
.
Обычно, выбирается переменная с большим
абсолютным значением отрицательного
коэффициента в “
- уравнении”. Пусть это будет
.
можно получить, увеличивая
или
.
Обычно, выбирается переменная с большим
абсолютным значением отрицательного
коэффициента в “
- уравнении”. Пусть это будет
.
В качестве исключаемой переменной выбирается та, которая первой обратится в ноль при увеличении . Вычисляем отношения постоянных в правой части к коэффициентам при . Исключаемой будет та переменная, для которой это отношение минимально (но не отрицательно и не ноль).
1-й полушаг.
-
Б
1
0
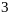
1

0
0
4
2
1
0
1
0
0
8
0
3
0
1
2
0
10
0
2
0
0
0
2
4
0
-1
0
3
0
0
24
2–й полушаг.
1-я итерация жорданова преобразования.
-
Б
1
0

1
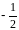
0
0
2

1

0
0
0
4
8
0
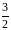
0
1
0
5
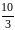
0
1
0
0
0
1
2
2
0
0
0
0
12
Этот
план по-прежнему не оптимален, так как
в строке целевой функции остается
отрицательный коэффициент при
.
То есть
будет вводится в базис. Исключаемой из
базиса переменной становится
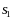 .
.
1–й полушаг.
-
Б
1
0

1
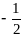
0
0
2
0
1
0
0
5
0
0
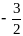
0

0
0
-1
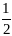
0
1
0
0
2
0
0
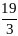
2-й полушаг.
2-я итерация жорданова преобразования.
-
Б
1
0
1
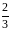
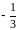
0
0
1
0
0
0
0
0
1
1
1
0
3
0
0

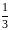
0
1
0
0
0
0
Мы
получили оптимальное решение.
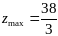 при
при
 .
.