Вариант 2

1. Теоретический вопрос:Методы сокращения избыточности в системах передачи информации. Сплайн-интерполяция.

2. Имеем Марковский источник с матрицей переходных вероятностей

Найти (Х), H₂(X), Н(Х/X^∞).

Построить коды Хаффмана для ансамблей X, X².

Указать наилучший алгоритм кодирования для данного источника.

3. Определить частоты появления букв в поговорке, построить для заданных частот код Хаффмана, найти среднюю длину кодовых слов, определить затраты на передачу поговорки при заранее известных частотах появления букв.

ехал грека через реку, видит грека в реке рак

Вариант 3

1. Теоретический вопрос: Кодирование дискретной информации при отсутствии помех.

2. Имеем Марковский источник с матрицей переходных вероятностей

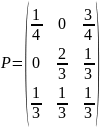
Найти Н(Х), H₂(X), Н(Х/X^∞).

Построить коды Хаффмана для ансамблей X, X².

Указать наилучший алгоритм кодирования для данного источника.

3. Определить частоты появления букв в поговорке, построить для заданных частот код Хаффмана, найти среднюю длину кодовых слов, определить затраты на передачу поговорки при заранее известных частотах появления букв.

сунул грека руку в реку, рак за руку греку цап

Вариант 4

1. Теоретический вопрос: Теоремы Шеннона о передаче сигналов по каналам связи.

2. Имеем Марковский источник с матрицей переходных вероятностей

Найти Н(Х), H₂(X), Н(Х/X^∞).

Построить коды Хаффмана для ансамблей X, X².

Указать наилучший алгоритм кодирования для данного источника.

3. Определить частоты появления букв в поговорке, построить для заданных частот код Хаффмана, найти среднюю длину кодовых слов, определить затраты на передачу поговорки при заранее известных частотах появления букв.

помучишься, так научишься

Вариант 5

1. Теоретический вопрос: Помехоустойчивое кодирование. Понятие и классификация помехоустойчивых кодов.

2. Имеем Марковский источник с матрицей переходных вероятностей

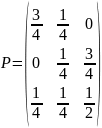
Найти Н(Х), H₂(X), Н(Х/X^∞).

Построить коды Хаффмана для ансамблей X, X².

Указать наилучший алгоритм кодирования для данного источника.

3. Определить частоты появления букв в поговорке, построить для заданных частот код Хаффмана, найти среднюю длину кодовых слов, определить затраты на передачу поговорки при заранее известных частотах появления букв.

либо дождик, либо снег, либо любит, либо нет

Вариант 6

1. Теоретический вопрос:Цифровое кодирование непрерывных сообщений.

2. Имеем Марковский источник с матрицей переходных вероятностей

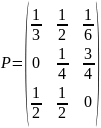
Найти Н(Х), H₂(X), Н(Х/X^∞).

Построить коды Хаффмана для ансамблей X, X².

Указать наилучший алгоритм кодирования для данного источника.

3. Определить частоты появления букв в поговорке, построить для заданных частот код Хаффмана, найти среднюю длину кодовых слов, определить затраты на передачу поговорки при заранее известных частотах появления букв.

На острую косу много и покосу! Покоси-ка коса!