1.3.Стационарные источники. Энтропия стационарного источника

ПустьА = {a₁, a₂, … , а_k} — конечный алфавит. Рассмотрим в качестве пространства событий Ω множество бесконечных (в обе стороны) последовательностей букв алфавитаА, т. е.Ω= А^∞. ПустьS_i^jпринадлежитА^∞состоит из последовательностей, имеющих наj-ом месте буквуа_i. Яс­но, что множествоS^j= {S_i^j }_i=1...k является разбиениемА^∞[8].

ИсточникS определяется как множество разбиенийS^j с совокупностью всевозможных условных вероятностей элементов разбиенийp(S_i0 ^j0 | S_i1 ^j1...S_in^jn) и p(S_i^j).

ИсточникSназывается стационарным, если вероятностиp(S_i0 ^j0 | S_i1 ^j1...S_in^jn) и p(S_i^j) независимы относительно сдвигов, т. е. справедливы равенства

p(S_i0 ^j0/S_i1 ^j1...S_in^jn) = p(S_i0⁰/S_i1 ^j1-j0...S_in^jn-j0),

p(S_i^j0)= p(S_i⁰).

ЕслиS — стационарный источник, то событияS_i1¹,S_i1² …S_inⁿ обычно отождествляются с соответствующими наборами буквa_i1, a_i2, … , а_inи вместоp(S_in^j+n/S_i0 ^jS_i1 ^j+1...S_in-1 ^jn-j0)пишут p(a_in/a_i0a_i1 … а_in-1), подразумевая под этим вероятность появления буквы а_in после набора букв a_i0a_i1 … а_in-1.

Энтропией стационарного источника Sназывается величина

H(S)= limH(S^п/S¹S²...S^n-1).

Стационарный источникS называется источником Бернулли, если p(S_i^j/S_i1 ^j1S_i2 ^j2...S_in^jn) = p(S_i^j). Другими словами,S — источник Бернулли, если вероятность появления буквы не зависит ни от места в по­следовательности, ни от предыдущих букв. Для источника Бернулли новое определение энтропии совпадает с определением, использовавшимся ранее [8, 9]:

Стационарный источник S называется Марковским источником r-го порядка, если

p(S_i^j/S_in^j-nS_in-1 ^j-n+1...S_i1 ^j-1)=

= p(S_i^j/S_ir ^j-rS_ir-1^j-r+1... S_i1 ^j-1)

приr≤ п. Другими словами, вероятность появления следующей буквы зависит только отr предыдущих. ЕслиS — Марковский источник r-го порядка, то

H(S) =H(S^r+1/S¹ S²... S^r) =

= –∑p(S_i1¹S_i2² ...S_ir^rS_ir+1^r+1)log p(S_ir+1^r+1/S_i1¹

i_1…i_r+1

S_i2²...S_ir^r)=

₌ –∑p(a_i1… а_ir+1) log p(а_ir+1/a_i1… а_ir).

i_1…i_r+1

Пронумеруем подряд все возможные слова из г букв s_i = a_i1 ...a_ir. Слова s_i называются состояниями Марковского источника Sr-го порядка. При появлении каждой новой буквы источник S переходит в новое состояние

s_i = a_i1 ...a_{ir →} s_j = a_i2 ...a_ir+1

Можно определить Марковский источник общего вида, состояния которого не связаны с наборами из фиксированного числа букв.

Марковский источник называется эргодическим, если вероятность перехода через произвольное (большее некоторого фиксированного числа т число шагов из каждого состояния s_i в произвольное состояние s_j больше нуля.

Если для некоторого эргодического Марковского источника сп состояниями известны только вероятности перехода из одного состояния в другое, то вероятности его состояний можно получить из системы уравнений

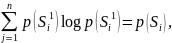
Пусть S — Марковский источник первого порядка с алфавитом {a₁, . . ., a_k}, и вероятности p(a_i/a_j) появления буквы щ вслед за буквой a_i записаны в матрице Q = {q_ij}, где q_ij =p(a_i/a_j). Тогда вероятности р(a_i) можно вычислить из уравнения Qp = р, где р = (р(а_i), . . . ,р(а_k)), учитывая, что ∑ p(a_i)=1.

Марковский источник можно полностью задать набором его состояний s₁, . . .,s_n, матрицей вероятностей перехода из одного состояния в другое p(s_i / s_j) и набором вероятностей порождения букв в каждом из состоянийp(a₁ / s_j), . . . ,p(a_k / s_j), 1 < j < п. Если считать, что после­довательности, порождаемые источником, бесконечны только в однусторону, т. е. имеют начало, то для полного определения источника нужно задать еще начальное состояние.

Разделим бесконечную последовательность букв, порожденную Марковским источникомS с состояниями s₁, ..., s_n на n подпоследовательностей, каждая из которых состоит из букв, порожденных в определенном состоянии s_j. Поскольку вероятность появления очередной буквы зависит только от состояния источника, то буквы j-й последовательности появляются независимо друг от друга с вероятностями p(a_i/a_j). Имея в виду этот факт, говорят, что Марковский источник разделяется на п источников Бернулли, каждый из которых определяется набором условных вероятностей р(a₁/s_j), . . .,p(a_k/s_j), 1 ≤j≤ п, и обладает энтропией

Таким образом, получаем формулу для энтропии Марковского источника S с состояниями s₁, . . .,s_n:

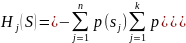
Таким образом, последовательность, порожденную Марковским источником, можно эффективно кодировать, разделяя ее по числу состояний на п подпоследовательностей и кодируя каждую из них отдельно любым из побуквенных кодов.

Применение Марковских цепей достаточно сильно упрощается, когда эти цепи гомогенны, стационарны и регулярны. Марковская цепь называется гомогенной (однородной), если вероятности переходов между состояниями не зависят от выбора временной точки отсчета, т.е. вероятности переходов зависят от разности временных отсчетов.

Гомогенная цепь Маркова является регулярной, если [1]:

1. Предельная матрица вероятностей перехода существует.

.

Причем всеn строк предельной матрицы представляют собой предельное распределение вероятностей состояний матрицы.

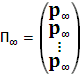
2. Предельное распределение вероятностей состояний p_∞ является единственным стационарным распределением вероятностей состояний любой регулярной цепи Маркова.

p_∞ = p₀

3.Цепь Маркова везде будет регулярной, если существует некоторое натуральное значение шага n, при котором все компоненты некоторого столбца матрицы вероятностей перехода на этом шаге n, будет отлично от нуля. Другими словами, цепь Маркова является регулярной если, на некотором шаге n существует по меньшей мере одно состояние, которое может быть достигнуто из любого начального состояния. Если в Марковской цепи вероятность очередного символа оказывает влияние на rпредыдущих символов, то говорят, что память такого источника охватываетr последовательных символов, а сам источник называют конечным дискретным Марковским источником с памятью r.

Заметим, что такой источник обладает свойством и эргодичности. Тогда конечный дискретный эргодический Марковский источник с памятью r полностью считается заданным (или определенным) следующими условиями:

1.Задано непустое множество состояний

, причем каждое состояние S_i содержит вектор длиной r .

2. Каждое состояние S_iсоответствует дискретному источнику без памяти с алфавитом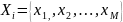 и вероятностями j-ых символов алфавита

.

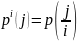3. Задано начальное распределение вероятностей состояний

p₀ = (p₀(1), p₀(2), …, p₀(N)).

4. СостояниеS[n], образованное изr-1 последовательных символов, после добавления очередного символаX[n] переходит в состояние S[n+1].

Энтропия стационарного эргодического Марковского источника вычисляется исходя из того, что некоторое состояние источникаS_i является как бы подисточником без памяти, обладающим в свою очередь соответствующей энтропией. Тогда энтропия первоначального источника равна математическому ожиданию энтропии подисточников. Таким образом, стационарный эргодический Марковский источник с алфавитом из М символов, имеющий n состояний, т.е. N подисточников без памяти энтропия каждого из которых равна

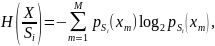
где – вероятность символа X_m при условииS_i состояния, обладает энтропией, равной математическому оживанию энтропии подисточника.

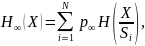
где p_∞ – предельное распределение вероятностей состояний.

Таким образом, приt→∞ в системе S устанавливается некоторый предельный стационарный режим: хотя система случайным образом и меняет свои состояния, но вероятность каждого из них не зависит от времени и каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Это свойство позволяет обходиться при нахождении параметров системы на основе моделирования одной достаточно длинной реализацией.

Для вероятностей p₁(t), p₂(t),…, p_n(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова, которые в случае нахождения предельных вероятностей превращаются в систему линейных алгебраических уравнений для каждого состояния. Совместно с нормировочным условием эти уравнения дают возможность вычислить все предельные вероятности.

Общее правило составления уравнений Колмогорова для предельных вероятностей p_i(t) можно сформулировать следующим образом:

• в левой части уравнения стоит сумма произведений вероятностей всех состояний, из которых идут стрелки в i-ое состояние, на интенсивности соответствующих потоков минус сумма интенсивностей всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния;

• в правой части уравнения стоит 0.