- •Вопрос №21 Динамическая остойчивость. Диаграмма динамической остойчивости и ее свойства.
- •Вопрос №22 Определение динамического угла крена и опрокидывающего момента по диаграмме динамической остойчивости.
- •Вопрос №23 Требования регистра к остойчивости морских судов.
- •Вопрос №24 Непотопляемость судна. Мероприятия по обеспечению непотопляемости
- •Вопрос №25 Принципы обеспечения непотопляемости морских судов
- •Вопрос №26 Расчет непотопляемости методом постоянного водоизмещения
- •Вопрос №27 Расчет непотопляемости методом приема груза
- •Вопрос №28 Расчет непотопляемости при затоплении группы отсеков
- •Вопрос №29 требования регистра к непотопляемости морских судов
- •Вопрос №33 Непотопляемость. Коэффициенты проницаемости. Категории затопления отсеков.
- •Вопрос №37 Управляемость. Силы и моменты, действующие на судно при криволинейном движении.
- •Вопрос №38 Периоды и параметры циркуляции судна.
- •Вопрос №41 Диаграмма Ремеза. Ее использование.
Вопрос №21 Динамическая остойчивость. Диаграмма динамической остойчивости и ее свойства.
Динамической остойчивостью называют способность судна выдерживать, не опрокидываясь, динамическое воздействие кренящего момента.
Диаграмма динамической остойчивости. Кривую, выражающую зависимость работы восстанавливающего момента (или плеча динамической остойчивости) от угла крена, называют диаграммой динамической остойчивости.
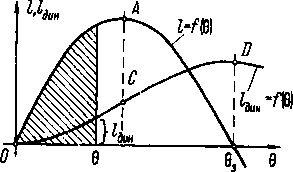 Рис.
2.33. Диаграммы статической и динамической
остойчивости
Рис.
2.33. Диаграммы статической и динамической
остойчивости
Формулы (2.85) и (2.86) показывают, что диаграмма динамической остойчивости является интегральной кривой по отношению к диаграмме статической остойчивости (рис. 2.33) и поэтому обладает следующими свойствами, общими для всех интегральных кривых:
- точки пересечения подынтегральной кривой (диаграммы статической остойчивости) с осью абсцисс отвечают точкам О и D экстремума интегральной кривой (диаграммы динамической остойчивости);
- точка А максимума диаграммы статической остойчивости соответствует точке перегиба С диаграммы динамической остойчивости;
- любая ордината диаграммы динамической остойчивости, отвечающая некоторому углу крена θ, представляет в масштабе соответствующую этому углу крена площадь диаграммы статической остойчивости (заштрихована на рисунке).
Вопрос №22 Определение динамического угла крена и опрокидывающего момента по диаграмме динамической остойчивости.
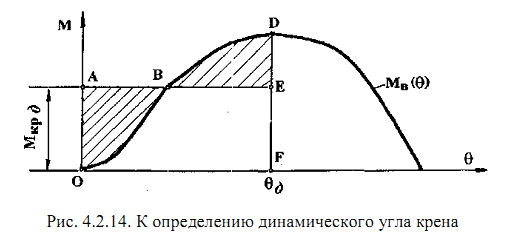
Наибольший угол динамического крена 9д определяется из условия равенства работ кренящего и восстанавливающего моментов.
Из курса теоретической механики известно, что работа пары сил выражается произведением ее момента на угол поворота, а при переменном моменте -площадью под его графиком, построенном в функции от угла поворота. Следовательно, площадь под графиком Мв = /(#) представляет собой работу Тв восстанавливающего момента, а так как математически площадь выражается определенным интегралом, то
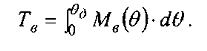
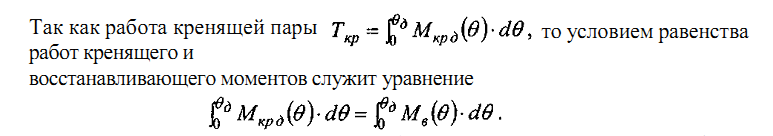
Решение этого уравнения может быть получено только лишь графическим способом, т.е. подбором ординаты DF, как показано на рис. 4.2.14, при которой площадь OAEF равна площади OBDF. Но учитывая то, что площадь OBEF общая, то для уравнивания работ необходимо уравнять лишь заштрихованные площади.
Построенная перед предстоящим рейсом диаграмма статической остойчивости позволяет определить еще до отхода тот наибольший динамически приложенный кренящий момент, который судно способно выдержать на переходе, не опрокинувшись (обычно его называют опрокидывающим моментом Мопр, а его плечо - / ), и соответствующий ему предельный динамический угол крена 9д д. Для этого необходимо уравнять площади S^ = S2,
как показано на рис. 4.2.15.
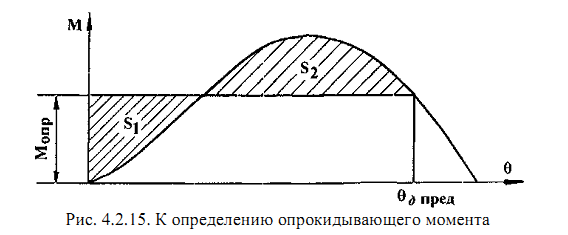
Ввиду жизненной важности, определение опрокидывающего момента является обязательным при проверке остойчивости судна перед предстоящим выходом в море с последующим его сравнением с динамически приложенным кренящим моментом от ветрового давления Мкрд (см. выше) по так называемому критерию погоды - К.
Согласно требованиям правил Российского Морского Регистра Судоходства его значение должно удовлетворять условно