Вопрос №19

Диаграмма статической остойчивости. Кривую, выражающую за­висимость плеча статической остойчивости l или восстанавливающего момента М_В=Рl от угла крена θ называют диаграммой статической остойчивости или диаграммой Рида по имени английского корабель­ного инженера, впервые предложившего ее для оценки остойчивости судна на больших углах крена. По оси абсцисс диаграммы отклады­вают значения угла крена: положительные (на правый борт) вправо и отрицательные (на левый борт) влево от начала координат, а по оси ординат - значение плеча остойчивости или восстанавливающего момента (рис. 2.22). Поскольку диаграмму остойчивости строят для некоторого определенного водоизмещения судна, между плечом остойчивости и восстанавливающим моментом существует прямая пропорциональная зависимость и, следовательно, одна и та же кривая может служить одновременно диаграммой моментов и диаграммой плеч остойчивости - изменяется только масштаб ее ординат. В таких случаях говорят, что диаграмма остойчивости построена „в плечах" или „в моментах".

Рис. 2.22. Диаграмма статической ос­тойчивости

В силу симметрии судна относительно ДП обычно ограничиваются построением только одной половины диаграммы остойчивости для положительных значений угла крена - на правый борт.

Остойчивость на малых углах крена можно рассматривать, очевид­но, как частный случай остойчивости на больших углах крена. Следо­вательно, диаграмма статической остойчивости должна характеризо­вать некоторым образом также начальную поперечную остойчивость судна. Действительно, дифференцируя по углу крена θ приближенную (метацентрическую) формулу для плеча статической остойчивости l ≈ h sin θ, получаем

(2.72)

При θ = 0 эта производная принимает точное значение:

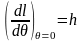(2.73)

Таким образом, в начальном (прямом) положении судна производная плеча статической остойчивости по углу крена численно равна началь­ной поперечной метацентрической высоте.

Но, как известно из аналитической геометрии, производная функ­ции геометрически выражает угловой коэффициент касательной в дан­ной точке к графику функции, т. е. тангенс угла между этой касатель­ной и положительным направлением оси абсцисс. Следовательно, для изображения начальной метацентрической высоты на диаграмме плеч статической остойчивости можно воспользоваться следующим по­строением (рис. 2.23): по оси абсцисс откладывают от начала координат отрезок ОА, равный в масштабе углов крена 1 рад, затем в точке А вос­станавливают перпендикуляр к оси абсцисс, который пересекается в точке В с касательной к диаграмме, проведенной в начале координат. Отрезок АВ этого перпендикуляра, измеренный в масштабе плеч остойчивости, будет равен начальной метацентрической высоте. В са­мом деле, из прямоугольного треугольника ОБА находим

(2.74)

Соответственно, если диаграмма остойчивости построена в моментах, то производная восстанавливающего момента по углу крена при θ = 0 будет численно равна коэффициенту поперечной остойчивости k=Ph.

Рисунок 2.23 наглядно показывает допустимые пределы использо­вания метацентрической формулы (2.10), графиком которой является касательная 0В. При малых θ прямая ОВ и кривая ОСЕ, выражающая действительный закон изменения плеча статической остойчивости по углу Θ, практически совпадают. Резкое расхождение между ними начи­нается обычно после входа в воду кромки палубы или выхода из воды скулы судна.

Рис. 2.23. Начальная остойчи­вость на диаграмме статической остойчивости

При положительной начальной остойчивости характерными точка­ми диаграммы являются точка О - положение устойчивого равновесия судна - и точки В и В', расположенные симметрично относительно на­чала координат и определяющие углы заката диаграммы Θ₃, при кото­рых судно находится в положениях неустойчивого равновесия (см. рис. 2.22). При углах крена, меньших угла заката, судно остойчиво, по­скольку восстанавливающий момент стремится вернуть его в положе­ние устойчивого равновесия О. Наибольшую по абсолютному значению ординату диаграммы, определяемую точками А или А', называют мак­симальным плечом диаграммы (или максимальным восстанавливаю­щим моментом), а отвечающий этой ординате угол крена - углом мак­симума диаграммы остойчивости. Наибольшая ордината диаграммы соответствует предельному статическому кренящему моменту, при­ложение которого еще не вызывает опрокидывания судна.

На рис. 2.24 приведены типичные диаграммы статической остойчи­вости для низкобортного судна с большой начальной остойчивостью и высокобортного судна с малой начальной остойчивостью.

Рис. 2.24. Типичные формы диаграммы статической остойчивости: α — низко­бортного судна; б — высокобортного судна

На рис. 2.25 изображена диаграмма статической остойчивости судна, имеющего отрицательную начальную остойчивость (в прямом положении). В этом случае положениям неустойчивого равновесия судна будут отвечать не только точки заката диаграммы В и В', но и на­чало координат О. Положениям устойчивого равновесия будут соот­ветствовать две точки - С и С'. Таким образом, судно с отрицательной начальной остойчивостью не может свободно плавать в прямом по­ложении; оно будет иметь крен θ₁ на правый борт или равный ему крен θ’₁ на левый борт в зависимости от случайных внешних причин (ветра, волнения, перекладки руля и т. п.). Наличие отрицательной начальной остойчивости еще не может служить основанием для заклю­чения, что данное судно вообще неостойчиво и должно опрокинуться. Судно опрокидывается только в том случае, когда его диаграмма остойчивости примет вид, показанный на рис. 2.25 штриховой линией, и будет пересекать ось абсцисс только в одной точке - в начале коор­динат О.

Рис. 2.25. Диаграмма статической остойчивости

Построение диаграммы статической остойчивости и практическое ее использование

Задача о построении диаграммы статической остойчивости с ис­пользованием ЭВМ при максимальной автоматизации ввода исходных данных в принципе решена. Однако в настоящее время до осуществле­ния массового (серийного) изготовления бортовых ЭВМ с соответ­ствующими устройствами и снабжения ими судов морского флота для построения диаграмм статической остойчивости могут служить в ка­честве вспомогательных материалов интерполяционные кривые плеч остойчивости формы, пантокарены и универсальные диаграммы остой­чивости, содержащиеся в комплекте судовой документации.

Интерполяционные кривые плеч остойчивости формы и пантока­рены. При заданных обводах корпуса плечи формы l_ф можно рассмат­ривать как функцию двух переменных - объемного водоизмещения V и угла крена θ:

l_ф = f(V,θ). (2.75)

Если в уравнении (2.75) положить θ = θ_i = const, плечо формы ста­новится функцией одного переменного l_ф=f(V). Кривые l_ф=f(V) называют интерполяционными кривыми плеч остойчивости формы. Их строят в конструкторских бюро для ряда углов крена от 0 до 90° (с ин­тервалами 10°) для водоизмещении, лежащих в пределах, представ­ляющих практический интерес, т.е. от водоизмещения порожнего судна V_nop до водоизмещения судна с полным грузом V_гр (рис. 2.26).

С помощью интерполяционных кривых плеч остойчивости формы можно построить диаграмму статической остойчивости судна для любого состояния его нагрузки. Для этого на оси абсцисс интерполя­ционных кривых откладывают точку, соответствующую данному водоизмещению, восставляют в ней перпендикуляр и снимают с кри­вых значения l_ф для углов крена 10°, 20° и т. д. Дальнейшее вычисле­ние плеч статической остойчивости производят по формуле

l = l_ф – a sin θ = l_ф – (z_g-z_c)sin θ (2.76)

При этом аппликату ЦТ судна z_g находят из расчета нагрузки, отвечаю­щей данному водоизмещению, а аппликату ЦВ z_c - по соответствую­щей кривой, имеющейся в документе “Кривые элементов теоретичес­кого чертежа”. После определения всех плеч формы строят кривую l_ф и синусоиду α sin θ, разности ординат которых являются плечами ста­тической остойчивости (рис. 2.27).

Если плечи остойчивости формы l_ф отсчитываются от полюса Ε (см. рис. 2.21), то соответствующие кривые l_ф =f(V) носят название пантокарен. При помощи пантокарен диаграммы статической остойчивости строят так же, как при помощи кривых плеч остойчивости формы.

Практическое использование диаграммы статической остойчивос­ти.

Диаграмму статической остойчивости, построенную для данного состояния нагрузки судна, во-первых, используют для того, чтобы подтвердить выполнение требований Регистра СССР к остойчивости судна на больших углах крена, изложенных ниже. Такое подтвержде­ние может стать необходимым в тех случаях, когда нагрузка судна не соответствует типовой (предусмотренной Информацией об остой­чивости) и его остойчивость вызывает сомнения.

Рис. 2.29. Применение диаграм­мы статической остойчивости для определения угла крена судна при горизонтально-попе­речном переносе груза

Во-вторых, с помощью диаграммы статической остойчивости может быть определен крен судна тогда, когда метацентрическая формула, при­годная только для малых углов крена, оказывается неприменимой. Для нахождения угла крена на диаграмме статической остойчивости строят кривую кренящего момента М_кр =f(θ) или кренящего плеча l_кp = M_кp/P= f(θ). Точки пересечения этой кривой с диаграммой остойчи­вости определят положения устойчивого и неустойчивого равновесий судна. Например, кренящее плечо при горизонтально-поперечном переносе груза на расстояние у₂ – у₁ выражается зависимостью

l_кр=Р(y₂-y₁)соsθ/Р. (2.81)

Углу статического крена θ₁ (положение устойчивого равновесия) будет соответствовать точка А пересечения косинусоиды (2.81) с диаг­раммой остойчивости (рис. 2.29). Точка В определит угол θ₂, отвечаю­щий положению неустойчивого равновесия.