Вопрос №18

Остойчивость на больших углах наклонения

Общие положения. В процессе изложения теории начальной остой­чивости судна было отмечено, что определение восстанавливающего момента и плеча остойчивости метацентрическими формулами допус­тимо только при малых углах наклонения. При увеличении этих углов приходится прибегать к теории остойчивости на больших углах накло­нения. Основы данной теории излагаются в настоящем параграфе, где рассматривается лишь остойчивость на больших углах крена, посколь­ку большой дифферент у неповрежденного судна практически никогда не возникает.

Условимся, как и ранее, что в исходном равновесном положении судно сидит прямо и на ровный киль, его наклонение происходит в вертикальной поперечной плоскости, а деривационный момент, возникающий в процессе наклонения вследствие несимметрии судна относительно плоскости мидель-шпангоута уравновешивается некото­рым воображаемым внешним моментом. Другими словами, будем рассматривать плоскую задачу поперечного наклонения судна, счи­тая, что все характерные точки - ЦВ, ЦТ, метацентр, а также линии действия сил веса и плавучести представлены их проекциями на плоскость наклонения, совпадающую с координатной плоскостью yOz (рис. 2.21).

Рис. 2.21. Наклонение судна на боль­шой угол

Рассмотрим равнообъемное наклонение судна на угол Θ; не налагая на его значение каких-либо ограничений. При таком накло­нении ЦВ судна переместится в точку c_θ, а сила веса и сила плавучести γV, действуя пер­пендикулярно новой ватерлинии В_θЛ_θ, составят пару сил. Плечо этой пары 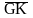= l, как и ранее, при рассмотрении ма­лых наклонений назовем плечом статической остойчивости, а момент М_в = Рl - восстанавливающим моментом судна.

При наклонении судна на большой угол теорема Эйлера недействи­тельна и ось наклонения уже не проходит через ЦТ площади начальной ватерлинии, отвечающей прямому положению судна. Кроме того, кривая СС_θ уже не может считаться дугою круга; аналитического вы­ражения она не имеет, и форма ее зависит от обводов судна. В общем случае поперечный метацентр m_θ выходит из ДП и его положение опре­деляется метацентрическим радиусом

r_θ =I_xθ /V, (2.69)

где I_xθ - центральный момент инерции площади наклонной ватерли­нии В_θЛ_θ относительно ее продольной оси.

Если из ЦВ опустить перпендикуляр CN на линию действия силы плавучести судна в его наклонном положении, то плечо остойчивости можно представить как разность:

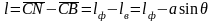. (2.70)

Отрезок l_ф называют плечом остойчивости формы, так как при данных водоизмещении судна и угле крена его значение зависит только от координат ЦВ, определяемых формой подводного объема. Отрезок l_в = α sinθ называют плечом остойчивости веса, так как при данном угле крена его величина зависит только от возвышения α ЦТ над ЦВ. Соответственно момент Мф=Рl_ф называют моментом остой­чивости формы, а момент М_В =Рl_В = Pa sin θ - моментом остойчивос­ти веса.

Иногда в качестве плеча остойчивости формы 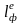принимают пер­пендикуляр ER, опущенный на линию действия силы плавучести из полюса Е, расположенного неподвижно в ДП судна. Тогда плечо остой­чивости веса равно = (z_g-z_e)sin θ, а плечо статической остойчи­вости

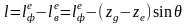. (2.71)

Рассмотренное выше разделение плеча остойчивости на две части имеет целью выделение той его части (плеча веса), которая зависит от данного состояния нагрузки судна и, следовательно, может быть определена только на судне после его погрузки. Оставшаяся же часть (плечо формы) может быть рассчитано заранее в функции водоизме­щения и угла крена, а результаты такого расчета могут быть выданы на судно в виде соответствующих графиков.