Вопрос №15

Поперечные горизонтальные перемещения не приводят к изменению остойчивости. При этом возникают лишь кренящие моменты.

Продольные горизонтальные перемещения. Как и поперечные, они не приводят к изменению остойчивости, но у судна возникает дифферент.

Вопрос №16

Влияние подвешенного груза на начальную остойчивость судна. Предположим, что находящийся в трюме груз массой т поднимают судовым краном или стрелой (рис. 2.14). В момент отрыва от настила трюма груз становится подвешенным, и в этот же момент начальная метацентрическая высота мгновенно получает некоторое приращение δh. Для определения этого приращения мысленно наклоним судно на малый угол Θ. Тогда шкентель, на котором подвешен груз, примет положение, перпендикулярное плоскости наклонной ватерлинии, а ЦТ груза g переместится в положение g₁. Перемещение груза можно пред­ставить как приложение к судну двух противоположно направленных вертикальных сил p = mg в точках g и g₁. Эти силы создают пару сил на плече l sin θ, где l - длина линии подвеса от нока стрелы О до ЦТ груза g. Момент этой пары δ М = рl sin θ уменьшает первоначальный восста­навливающий момент судна M_B=Phsinθ, действовавший до отрыва груза от настила трюма. Восстанавливающий момент судна с подве­шенным грузом равен

M_В1 = М_В - δМ = Р(h-pl/P)sinθ (2.35)

Рис. 2.14. Подвешенный груз

Из формулы (2.35) видно, что в момент отрыва поднимаемого груза от настила, т. е. в тот момент, когда он становится подвешенным грузом, метацентрическая высота изменяется на величину

δh = -pl/P = -ml/Δ (2.36)

Из сравнения формул (2.36) и (2.27) следует, что влияние на остой­чивость судна подвешенного груза равносильно влиянию подъема груза по вертикали на расстояние l, т. е. мгновенного перемещения его ЦТ в точку подвеса. Таким образом, дальнейший подъем груза на шкентеле после отрыва его от настила уже не сказывается на остой­чивости судна.

Вопрос №17

Влияние свободной поверхности жидкого груза на начальную остойчивость судна. На каждом судне размещается значительное коли­чество жидких грузов (топлива, воды, смазочного масла) в цистернах (танках). Для наливных транспортных судов (танкеров) жидкий груз является основным перевозимым грузом. Если жидкий груз заполняет цистерну полностью, т. е. цистерна запрессована, то для задач статики он ничем не отличается от любого твердого груза такой же массы. Однако если жидкий груз заполняет лишь часть цистерны и, следова­тельно, имеет свободную поверхность, то он получает возможность переливаться при наклонении судна. В результате этого изменяется форма объема жидкости в цистерне и перемещается ЦТ судна, что отражается на его остойчивости.

Предположим, что в одном из отсеков судна, первоначально за­прессованном, остался жидкий груз с удельным весом γ_ж, который в прямом положении судна заполняет отсек до уровня вл, имея объем υ (рис. 2.15). Если мы наклоним мысленно судно на малый угол Θ, то свободная поверхность жидкости в отсеке также наклонится и займет положение в₁л₁, параллельное наклонной ватерлинии В₁Л₁, а ЦТ жид­кости g переместится в новое положение g₁. Вследствие малости угла θ можно считать, что перемещение ЦТ жидкости происходит по дуге круга радиусом l с центром в точке m₀, в которой пересекаются линии действия силы веса жидкого груза до и после наклонения судна. Как и в случае подвешенного твердого груза, переливание жидкого груза можно представить как приложение к судну двух противоположно направленных вертикальных сил Р = γ_ж υ . Эти силы создают, пару сил с плечом lsinθ, момент которой δМ = γ_жυlsinθ уменьшает первона­чальный восстанавливающий момент M_B=Phsinθ. Таким образом, с учетом переливания жидкости в отсеке восстанавливающий момент судна равен

M_В1 = Phsinθ - γ_жυlsinθ = P(h-γ_жυl/P) sinθ (2.37)

Рис. 2.15. Влияние свободной поверх­ности жидкого груза на начальную ос­тойчивость судна

Сравнивая рис. 2.1 и 2.15, видим, что точку m₀ можно рассматри­вать как метацентр жидкости в цистерне. Соответственно отрезок l = m₀g является ее метацентрическим радиусом и поэтому может быть определен формулой, аналогичной формуле (2.5):

I = i_x/υ, (2.38)

где I_Х - центральный момент инерции свободной поверхности жидкос­ти в цистерне относительно продольной оси (параллельной координат­ной оси Ох). Подставив выражение (2.38) в формулу (2.37), получим

M_В1 = P(h-γ_ж i_x /P) sinθ (2.39)

Как видно из уравнения (2.39), изменение начальной метацентрической высоты, отражающее переливание жидкости, может быть выраже­но формулой

δh = -γ_ж i_x /Р = -ρ_жi_х/Δ. (2.40)

Из выражения (2.40) следует, что при расходовании жидкого груза из запрессованных цистерн и появлении свободной поверхности всегда уменьшается остойчивость судна и что уменьшение метацентрической высоты не зависит от количества жидкого груза, поскольку в выражение для поправки δh не входит его объем υ.

Если на судне расходуется с образованием свободных поверхнос­тей несколько жидких грузов в отдельных, не сообщающихся между собой цистернах, то в формулу (2.40) вместо произведения ρ_жi_х следует подставить сумму 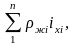где n - число отсеков с жидким грузом.

При возникновении свободных поверхностей в большом числе цистерн отрицательное приращение δh может оказаться по абсолютно­му значению столь велико, что начальная поперечная остойчивость судна станет отрицательной. Поэтому во избежание потери начальной остойчивости недопустимо одновременно расходовать жидкий груз из большого числа запрессованных цистерн (или принимать его одновре­менно в несколько порожних цистерн). Имеющиеся на судах Инструк­ции по приему и расходованию жидких грузов устанавливают опреде­ленный порядок расходования жидких грузов каждого вида (топлива, воды). Согласно этим инструкциям жидкость разрешается выкачивать из одной цистерны (или из одной пары цистерн правого и левого бор­тов) до полного их опорожнения, а затем переходить к расходованию из следующей цистерны и т. д. Прием жидких грузов производится в том же порядке, причем в каждую цистерну жидкость принимают до полной ее запрессовки.

Следует иметь в виду, что если в цистерне имеется лишь очень тонкий слой жидкости, объем которой составляет менее 5 % объема цистерны (рис. 2.16, а), или цистерна заполнена почти доверху, т.е. объем жидкости составляет более 95 % объема цистерны (рис. 2.16, б), то ширина свободной поверхности b_θ начинает резко уменьшаться после наклонения судна до некоторого весьма малого предельного угла крена θ_пред. Соответственно резкое уменьшение будет претерпе­вать и момент инерции свободной поверхности, а следовательно, и по­правка к метацентрической высоте. В таких случаях говорят, что влияние свободной поверхности приводит к недейственной потере ос­тойчивости, которую практически можно не учитывать при опреде­лении крена судна по метацентрической формуле.

Рис. 2.16. Случай недейственной потери остойчивости

Появление свободной поверхности жидкого груза влияет также и на продольную остойчивость судна. Поправка к продольной метацен­трической высоте будет определяться формулой

δH = -ρ_жi_у/Δ, (2.41)

где i_y - центральный момент инерции свободной поверхности жидкос­ти относительно поперечной оси (параллельной координатной оси Оу). Однако ввиду значительной величины продольной метацентрической высоты H, превышающей примерно на два порядка величину попереч­ной метацентрической высоты, поправкой δH обычно пренебрегают.