
Принцип суперпозиции электрических полей
Тонкий бесконечный диэлектрический стержень согнут под углом а = 90°. Одна сторона угла заряжена положительным зарядом с линейной плотностью τ = 1 нКл/м, а другая - отрицательным зарядом с такой же линейной плотностью. Определите напряженность электрического поля в точке, находящейся на биссектрисе угла на расстоянии R = 10 см от его вершины.
Тонкий стержень длиной L = 10 см равномерно заряжен с линейной плотностью τ = 1 мкКл/м. На продолжении оси стержня на расстоянии d = 20 см от ближайшего его конца находится точечный заряд Q = 100 нКл. Определите силу взаимодействия стержня и точечного заряда.
Тонкое полукольцо радиусом R = 20 см заряжено равномерно зарядом Q = 0,7 нКл. Найдите модуль вектора напряженности электрического поля в центре кривизны этого полукольца.
Тонкий очень длинный стержень равномерно заря жен с линейной плотностью заряда τ = 10 мкКл/м. На перпендикуляре к оси стержня, восставленном из его конца, находится точечный заряд Q = 10 нКл. Расстояние от заряда до конца стержня равно 20 см. Какая сила действует на точечный заряд?
Тонкое кольцо радиусом R = 8 см несет равномерно распределенный заряд с линейной плотностью τ = 10 нКл/м. Какова напряженность электрического поля в точке, равноудаленной от всех точек кольца на расстояние а = 10 см?
Тонкий стержень согнули так, что образовался равносторонний треугольник со стороной b = 10 см. На стержне расположен заряд с линейной плотностью, равной т= 10 нКл/м. Определите потенциал электрического поля в центре треугольника.
Одна половина тонкого прямого стержня имеет положительный заряд с линейной плотностью, равной х = 10 нКл/м, а другая - отрицательный заряд с такой же линейной плотностью. Длина всего стержня b = 20 см. На перпендикуляре к оси стержня, восставленном из его середины, находится положительный точечный заряд Q = 1 нКл. Определите силу, действующую на этот заряд.
Тонкая бесконечная нить согнута под углом а = 90°. Нить несет заряд, равномерно распределенный с линейной плотностью τ = 1 мкКл/м. Определите силу, действующую на точечный заряд Q = 0,1 мкКл, расположенный на продолжении одной из сторон и удаленный от вершины угла на 50 см.
Тонкая квадратная рамка равномерно заряжена с линейной плотностью т = 0,2 нКл/м. Определите потенциал электрического поля в точке пересечения диагоналей.
По тонкой нити, изогнутой по дуге окружности радиусом R = 10 см, равномерно распределен заряд Q = 20 нКл. Определите напряженность электрического поля, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.
Электрическое поле создано тонким стержнем, несущим равномерно распределенный заряд с линейной плотностью τ = 0,1 мкКл/м. Определите потенциал электрического поля в точке, удаленной от концов стержня на расстояние, равное длине стержня.
Тонкий провод длиной 20 см согнут посередине под прямым углом и равномерно заряжен с линейной плотностью τ = 10 нКл/м. Определите потенциал электрического поля в точке, удаленной от концов стержня на расстояние а = 10 см.
Найдите напряженность электрического поля в той же точке по условию задачи 30.12.
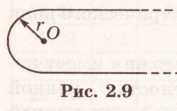 Равномерно заряженная
нить с линейной плотностью τ=10 нКл/м,
имеет конфигурацию, показанную на рис.
2.9. Радиус закругления r
= 10 см. Найдите напряженность электрического
поля в точке О, считая радиус закругления
значительно меньше длины нити.
Равномерно заряженная
нить с линейной плотностью τ=10 нКл/м,
имеет конфигурацию, показанную на рис.
2.9. Радиус закругления r
= 10 см. Найдите напряженность электрического
поля в точке О, считая радиус закругления
значительно меньше длины нити.По тонкому кольцу радиусом R = 20 см равномерно распределён заряд с линейной плотностью, равной т = 10 нКл/м. Определите потенциал электрического поля в точке, лежащей на оси кольца на расстоянии а = 5 см от центра.
На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью, равной τ = 10 нКл/м. Вычислите потенциал, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
Тонкий стержень согнули так, что образовалась квадратная рамка со стороной b = 10 см. Одна сторона квадрата несет положительный заряд с линейной плотностью τ = 10 нКл/м, противоположная сторона несет отрицательный заряд с такой же линейной плотностью. Остальные стороны не заряжены. Определите напряженность электрического поля в центре квадрата.
Определите потенциал электрического поля в центре шестиугольной равносторонней рамки, имеющей электрический заряд с линейной плотностью τ = 1 нКл/м.
Тонкая нить изогнута по дуге окружности радиусом R = 10 см и несет отрицательный заряд с линейной плотностью τ = -10 нКл/м. Длина нити равна половине длины окружности. Определите потенциал электрического поля в центре окружности.
Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 10 нКл/м. Какова сила, действующая на точечный заряд Q = 10 нКл, находящийся на расстоянии а = 20 см от стержня вблизи его середины? (Решить с помощью принципа суперпозиции.)
Тонкий длинный стержень равномерно заряжен с линейной плотностью τ = 10 нКл/м, Определите напряженность электрического поля в точке, находящейся на продолжении оси стержня на расстоянии 10 см от одного из его концов.
Определите напряженность электрического поля в центре тонкой квадратной рамки, если три стороны рамки имеют отрицательный заряд с линейной плотностью τ = -10 нКл/м, а четвертая не заряжена. Сторона квадрата 10 см.
Одну половину тонкого диэлектрического стержня зарядили положительным зарядом с линейной плотностью, равной τ = 10 нКл/м, а другую - отрицательным зарядом с такой же по модулю линейной плотностью. Определите потенциал электрического поля в точке, расположенной на продолжении оси стержня на расстоянии, равном половине его длины от конца стержня с положительным зарядом.
Две половины тонкого кольца заряжены разноименными зарядами с одинаковыми линейными плотностями τ = 10 нКл/м. Радиус кольца R = 10 см. Определите напряженность электрического поля в центре кольца.
Тонкий стержень равномерно заряжен с линейной плотностью τ = 10 нКл/м. Длина стержня равна L = 10 см. Определите напряженность электрического поля в точке, удаленной от концов стержня на расстояние, равное его длине.
Вычисление полей с помощью теоремы Гаусса
Рассматривая атомное ядро урана как равномерно заряженный по объему шар, определите потенциал электрического поля в центре ядра. Постройте график зависимости напряженности электрического поля от расстояния до центра ядра. Радиус ядра урана R = 1•10-14 м, заряд ядра Q = 92е = 147,2 • 10-19Кл (е = 1,6 • 10-19 Кл - элементарный заряд).
Пространство между двумя концентрическими сферами, радиусы которых Rx = 10 см и R2 = 20 см, заряжено с объемной плотностью р = -b/r, где b = 1 нКл/м, r - расстояние от центра сфер. Определите разность потенциалов между сферами. Постройте график зависимости напряженности электрического поля от расстояния до центра сфер.
Некоторая система имеет сферически симметричный заряд объемной плотностью р = р0 е , где р0 = = 1 нКл/м3, а = 10 м_3, г - расстояние от центра данной системы. Определите напряженность электрического поля в точке, находящейся на расстоянии R = 1 м от центра. Постройте график зависимости напряженности от расстояния до центра системы.
Шар радиусом R = 100 м имеет заряд Q = 10 нКл, однородно распределенный по его объему. Шар окружает среда, имеющая объемную плотность электрического заряда, зависящую от расстояния r до центра шара по закону р = р0(1 - r/R). Определите разность потенциалов между поверхностью шара и точкой, находящейся на расстоянии r = 2R от центра шара. Постройте график зависимости напряженности от расстояния до центра шара.
Шар радиусом R = 10 см имеет положительный заряд, объемная плотность которого зависит только от расстояния r до его центра по закону р = р0(1 - r/R), где р0 =10 нКл/м3. Определите разность потенциалов между центром и поверхностью шара. Постройте график зависимости напряженности от расстояния до центра шара.
Длинный цилиндр радиусом R = 2 см несет заряд, равномерно распределенный по его объему с плотностью р = 10 нКл/м3. Определите разность потенциалов между точками, отстоящими от оси цилиндра на расстояниях r1 = 1 см и r2 = 3 см. Постройте график зависимости напряженности от расстояния до оси цилиндра.
Большая плоская пластина толщиной d = 4 см имеет положительный заряд, равномерно распределенный по объему с объемной плотностью р = 10 нКл/м3. Определите разность потенциалов между поверхностью и точкой, находящейся внутри пластины на расстоянии b = 1 см от поверхности. Постройте график зависимости напряженности от расстояния до центра пластины.
Электрический ток, сила тока, плотность тока
Автомобильный электродвигатель-стартер в течение t = 3 с работал от батареи аккумуляторов при силе тока I1 = 150 А. Когда автомобиль двинулся в путь, генератор стал подзаряжать аккумуляторы при силе тока I2 = 4,5 А. За какое время восстановится прежнее состояние батареи?
Какой заряд проходит через сечение проводника, если известно, что сила электрического тока в этом проводнике равномерно возрастает от нуля до I = 5 А в течение t = 10 с?
Сила тока в цепи изменяется по закону I = I0 + at, где а = 2 А/с, I0 = 2 А. Определить заряд, который пройдет по проводнику за промежуток времени от = 0 до t2 = 2 с.
В медном проводнике, площадь сечения которого S = 0,17 мм2, сила тока I = 0,15 А. Определить плотность тока j в этом проводнике.
Сила тока в лампочке от карманного фонаря I = 0,32 А. Сколько электронов N проходит через поперечное сечение нити накала на время t = 0,1 с?
В электронно-вычислительной машине импульс тока от одного устройства к другому необходимо передать за время t = 10-9 с. Можно ли эти устройства соединить проводником длиной l = 40 см?
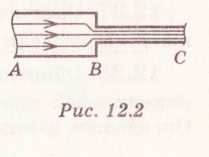 В
проводнике
переменного сечения (рис. 12.2) течет ток.
Одинакова ли напряженность электрического
поля на участках АВ
и ВС?
Одинакова ли средняя
скорость
направленного движения электронов
проводимости на обоих участках? Одинакова
ли сила тока на этих участках? Ответы
обосновать.
В
проводнике
переменного сечения (рис. 12.2) течет ток.
Одинакова ли напряженность электрического
поля на участках АВ
и ВС?
Одинакова ли средняя
скорость
направленного движения электронов
проводимости на обоих участках? Одинакова
ли сила тока на этих участках? Ответы
обосновать.Конденсатор емкостью С = 100 мкФ заряжают до напряжения 500 В за время t = 0,5 с. Каково среднее значение силы тока <I>?
Плоский конденсатор с площадью квадратных пластин S 400 см2 и расстоянием между ними d=2 мм подключён к источнику спряжением U = 120 В. В пространство между обкладками конденсатора со скоростью и = 10 см/с вдвигают пластину с диэлектрической проницаемостью ε = 2. Определить величину тока, протекающего в цепи.
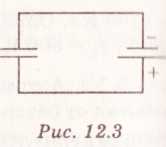 В
электрической цепи (рис. 12.3) после
зарядки конденсатора емкостью С
= 10-3
Ф, расстояние между обкладками которого
d
=
10 -2
м, напряжение 102
В, начинают сдвигать обкладки со
скоростью 10 см/с. Определить величину
и направление тока в цепи в момент
начала сдвига обкладок.
В
электрической цепи (рис. 12.3) после
зарядки конденсатора емкостью С
= 10-3
Ф, расстояние между обкладками которого
d
=
10 -2
м, напряжение 102
В, начинают сдвигать обкладки со
скоростью 10 см/с. Определить величину
и направление тока в цепи в момент
начала сдвига обкладок.Пластины плоского воздушного конденсатора, площадью 7,2 • 10-2 м2 каждая, подсоединены к источнику с ЭДС ε = 12 В. Одна из пластин движется навстречу другой таким образом, что расстояние между ними меняется по закону d = 0,1 -2t. Определить, как меняется сила тока в этой цепи. Вычислите I (t = 0).
Определить ток, создаваемый электроном, движущимся по орбите радиусом R = 0,5 • 10 -10 м в атоме водорода.
