Министерство образования и науки
России
Севастопольский государственный университет
РЕШЕНИЕ ЗАДАЧ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
ПРИ ИССЛЕДОВАНИИ ДИНАМИЧЕСКИХ СИСТЕМ
Методические указания
к выполнению лабораторной работы по дисциплине
«Математические основы теории систем»
для студентов дневной и заочной форм обучения
направления подготовки
27.03.04 – Управление в технических системах
Севастополь
2014
УДК 681.5
Решение задач одномерной оптимизации при исследовании динамических систем: Методические указания к выполнению лабораторной работы по дисциплине «Математические основы теории систем» для студентов дневной и заочной форм обучения по направлению подготовки 27.03.04 – Управление в технических системах / Сост. А.И.Грушун, Т.А.Грушун.- Севастополь: Изд-во СевГУ, 2014.- 9с.
В методических указаниях рассматриваются вопросы изучения и практического применения методов одномерной оптимизации, наиболее часто применяемых при анализе и синтезе динамических систем.
Методические указания предназначены для студентов дневной и заочной форм обучения направления подготовки 27.03.04 – Управление в технических системах .
Методические указания рассмотрены и утверждены на заседании кафедры технической кибернетики СевГУ, протокол №1 от 27 сентября 2014 г.
Допущено учебно-методическим центром СевГУ в качестве методических указаний.
Рецензент: Кожаев Е.А., канд. техн. наук, доцент, доцент кафедры кибернетики и
вычислительной техники СевГУ.
Содержание
1. |
Цель работы |
3 |
2. |
Краткие теоретические сведения |
3 |
3. |
Описание технических и программных средств выполнения работы |
7 |
4. |
Порядок выполнения теоретических расчетов |
7 |
5. |
Порядок выполнения экспериментальных исследований |
7 |
6. |
Содержание отчета о выполнении лабораторной работы |
8 |
7. |
Контрольные вопросы |
9 |
|
Библиографический список |
9 |
|
|
|
|
|
|
|
|
|
1. Цель работы
Освоить практическое применение основных методов одномерной оптимизации, применяемых в задачах исследования динамических систем.
2. Краткие теоретические сведения
При решении целого ряда задач теории автоматического управления возникает необходимость вычисления или уточнения значений точек пересечения частотных годографов динамических систем с осями координат комплексной плоскости. К таким задачам относится исследование устойчивости динамических систем по критериям Михайлова и Найквиста, построение областей устойчивости методами Д-разбиения и др. Наиболее применяемыми и подходящими для этих целей являются метод равномерного поиска и метод деления интервала пополам.
Рассмотрим метод равномерного поиска
[1]. Требуется найти безусловный минимум
функции f(x)
одной переменной, т.е. такую точку x*R,
что
.
Задается интервал унимодальности (начальный интервал неопределенности) L0=a0, b0 и количество вычислений функции N. Функция f(x) называется унимодальной на интервале L0=a0, b0, если она достигает глобального минимума на a0, b0 в единственной точке x* , причем слева от x* эта функция строго убывает, а справа от x* строго возрастает. Вычисления производятся в N равноотстоящих друг от друга точках (при этом интервал L0 делится на N+1 равных интервалов). Путем сравнения величин f(xi), i=1,…,N находится точка xk, в которой значение функции наименьшее. Искомая точка минимума x* считается заключенной в интервале xk-1, xk+1 (рисунок 1).
Рассмотрим алгоритм метода равномерного поиска.
Шаг 1. Задать начальный интервал неопределенности (интервал унимодальности) L0=a0, b0 и количество вычислений функции N.
Шаг 2. Вычислить точки
,
i=1,…,N,
равноотстоящие друг от друга.
Шаг 3. Вычислить значения функции в N найденных точках: f(xi), i=1,…,N.
Шаг 4. Среди точек xi,
i=1,…,N,
найти такую, в которой функция принимает
наименьшее значение:
.
Шаг 5. Точка минимума x* принадлежит интервалу: x*xk-1, xk+1=LN, на котором в качестве приближенного решения может быть выбрана точка x* xk.
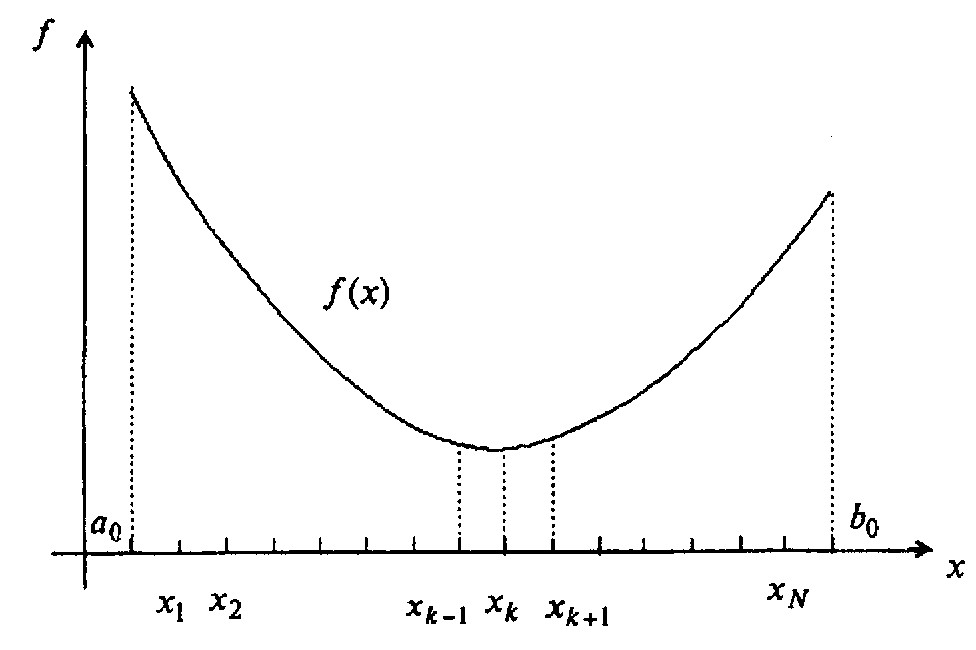
Рисунок 1 – Реализация метода равномерного поиска
Для метода равномерного поиска
характеристика относительного уменьшения
начального интервала неопределенности
находится по формуле
,
где N – количество
вычислений функции.
Если задана величина R(N),
то требуемое для достижения желаемой
точности количество вычислений функции
определяется как наименьшее целое
число, удовлетворяющее условию
.
Пример. Найти минимум функции f(x)=2x2-12x методом равномерного поиска на интервале унимодальности (начальном интервале неопределенности) L0=0, 10.
Воспользуемся алгоритмом равномерного поиска.
Зададим N=9 так, чтобы L0 содержал N+1=10 равных подынтервалов.
Определим точки вычисления функции:
,
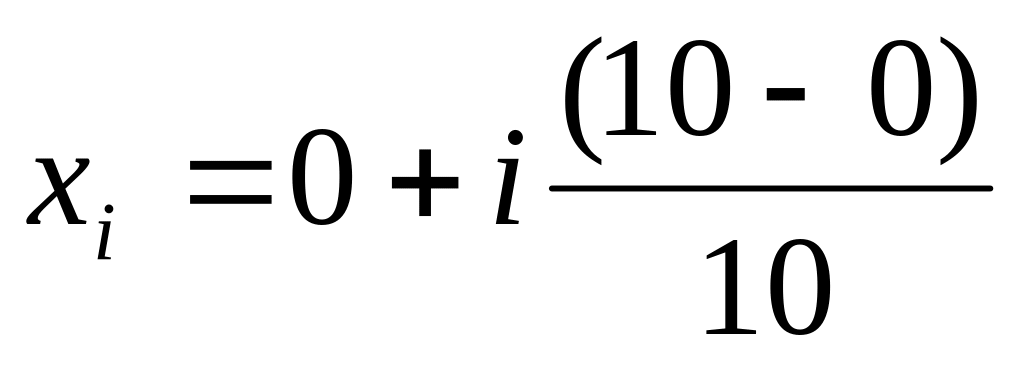i=1,…,9.Вычислим значения функции в девяти точках: f(1)=-10, f(2)=-16, f(3)=-18, f(4)=-16, f(5)=-10, f(6)=0, f(7)=14, f(8)=32, f(9)=54.
В точке x3=3 функция принимает наименьшее значение: f(x3)=-18.
Искомая точка минимума после девяти вычислений принадлежит интервалу:
x*2, 4=L9, в котором выбирается точка x* x3=3.
Заметим, что характеристика относительного
уменьшения начального интервала
неопределенности
.
Теперь рассмотрим метод деления интервала пополам [1]. Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку x*R, что .
Данный метод позволяет исключить из дальнейшего рассмотрения на каждой итерации в точности половину текущего интервала неопределенности. Задается начальный интервал неопределенности, а алгоритм уменьшения интервала основан на анализе величин функции в трех точках, равномерно распределенных на текущем интервале (делящих его на четыре равные части). Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Рассмотрим алгоритм метода деления интервала пополам.
Шаг 1. Задать начальный интервал неопределенности (интервал унимодальности) L0=a0, b0 и l0 – требуемую точность.
Шаг 2. Положить k=0.
Шаг 3. Вычислить среднюю точку
,
,
.
Шаг 4. Вычислить точки:
,
и
,
.
Заметим, что точки
делят интервал
на четыре равные части.
Шаг 5. Сравнить значения и :
а) если
,
исключить интервал
,
положив
,
.
Средней точкой нового интервала
становится точка
:
(рисунок 2а). Перейти к шагу 7;
б) если , перейти к шагу 6.
Шаг 6. Сравнить значения и :
а) если
,
исключить интервал
,
положив
,
.
Средней точкой нового интервала
становится точка
:
(рисунок 2б). Перейти к шагу 7;
б) если
,
исключить интервалы
,
,
положив
,
.
Средней точкой нового интервала
становится точка
:
(рисунок 2в).
Шаг 7. Вычислить
и проверить условие окончания:
а) если
,
процесс поиска завершается и
.
В качестве приближенного решения можно
взять середину последнего интервала:
;
б) если
l,
то положить k=k+1
и перейти к шагу 4.
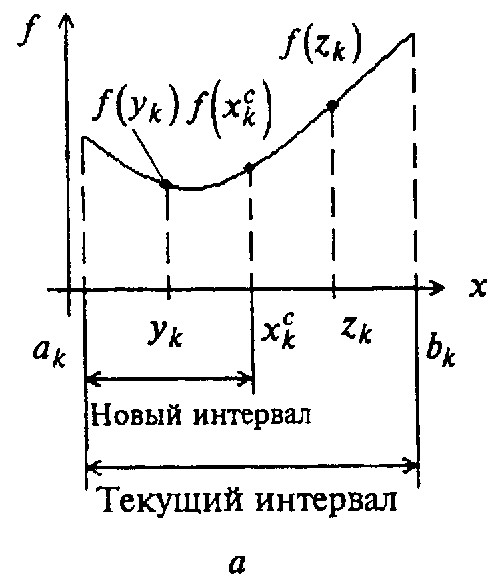
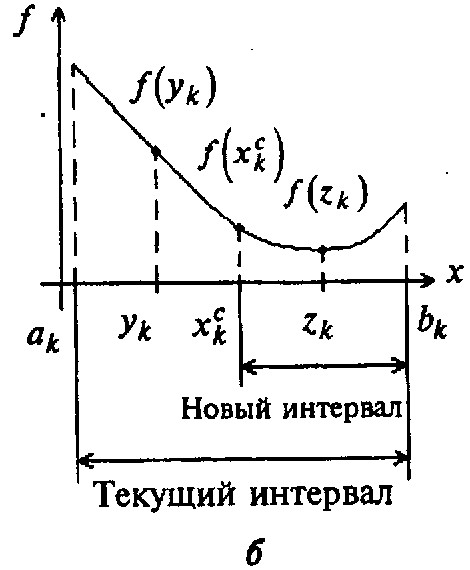
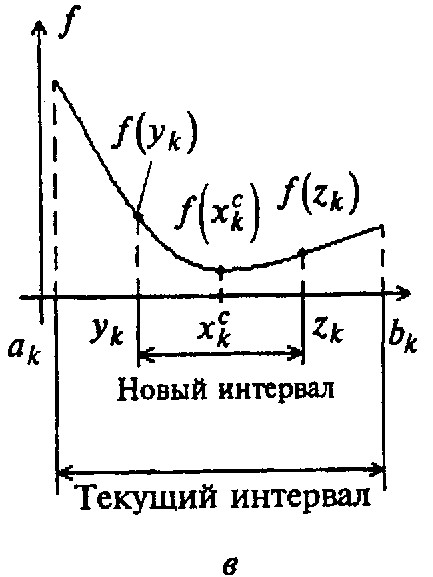
Рисунок 2 – Реализация метода деления интервала пополам
Для метода деления интервала пополам
характеристика относительного уменьшения
начального интервала неопределенности
находится по формуле
,
где N – количество
вычислений функции.
Если задана величина R(N),
то требуемое для достижения желаемой
точности количество вычислений функции
находится как наименьшее целое число,
удовлетворяющее условию
.
Также следует отметить, что текущие
интервалы имеют четные номера
,
где индекс указывает на сделанное
количество вычислений функции.
Пример. Найти минимум функции, рассмотренной в предыдущем примере, методом деления интервала пополам.
Воспользуемся алгоритмом деления интервала пополам.
Зададим начальный интервал неопределенности L0=0, 10. Пусть l=1.
Положим k=0.
30. Вычислим
.
40. Вычислим
.
50. Сравним
и
.
Так как
<
,
то положим
70. Получим
>l=1,
k=1. Переходим к шагу
4.
41. Вычислим
.
51. Сравним
и
.
Так как
>
,
то перейдем к шагу 6.
61. Сравним
и
.
Так как
>
,
то положим
71. Получим
>l=1.
Положим k=2 и переходим
к шагу 4.
42.Вычислим
.
52. Сравним
с
.
Так как
>
,
то перейдем к шагу 6.
62. Сравним
с
.
Так как
<
,
то положим
72. Получим
>l=1.
Положим k=3 и переходим
к шагу 4.
43. Вычислим
.
53. Сравним
и
.
Так как
>
,
то перейдем к шагу 6.
63. Сравним
и
.
Так как
>
,
то положим
73. Получим
<l=1;
.
В качестве решения можно взять среднюю
точку последнего интервала
.
Первые несколько итераций поиска изображены на рисунке 3.
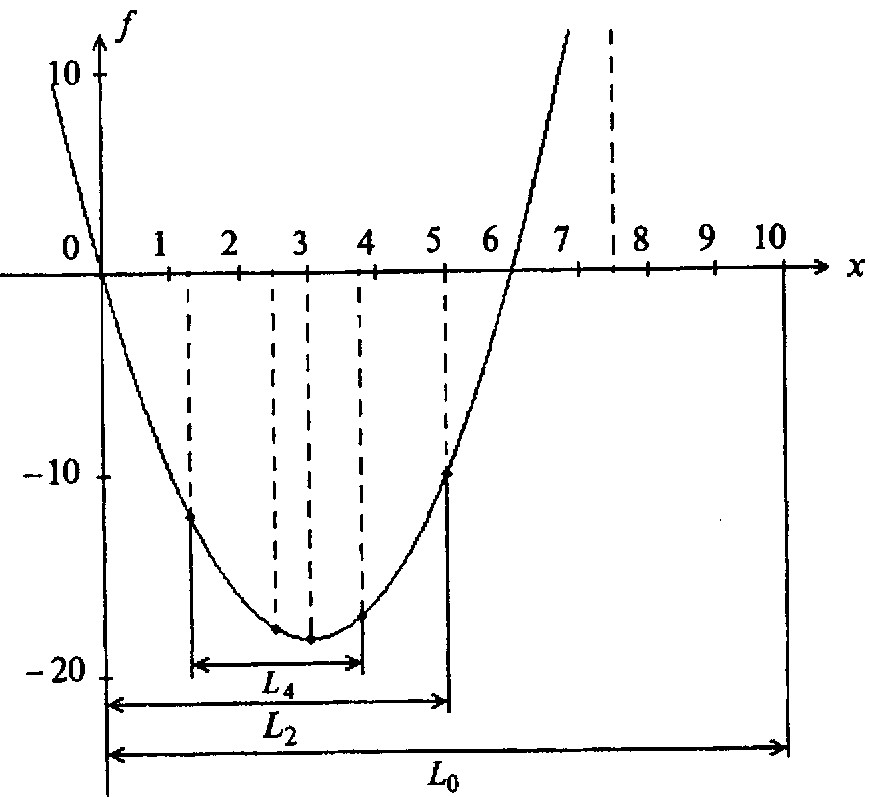
Рисунок 3 – Начальные итерации поиска минимума функции f(x)=2x2-12x методом
деления интервала пополам