2. Перестановки

Выберем из трех элементов a, b, c три элемента с учетом их расположения. Получим

a b с, b a с, b c а, c b а, a c b, c a b.

Составленные комбинации называются перестановками из трех элементов.

Перестановками из n элементов называются комбинации, которые состоят из всех n элементов и отличаются лишь порядком расположения этих элементов.

Иначе, перестановки – это размещения из n элементов по n. Нетрудно получить формулу для числа перестановок.

Теорема 1.4. Число перестановок из n различных элементов равно

(1.4)

Доказательство. Используем то, что перестановки – частный случай размещений. По формуле (1.2) получим

.

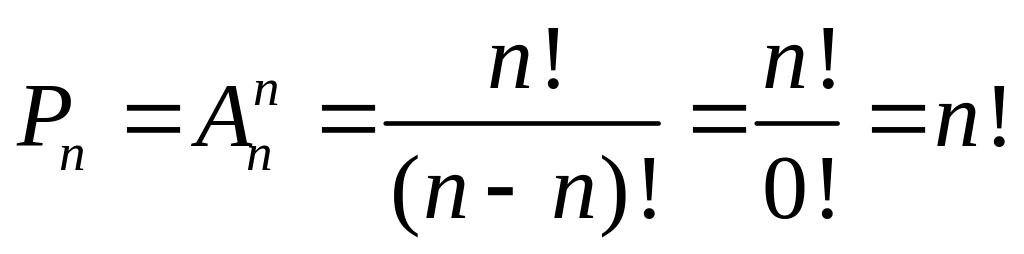Теорема доказана.

В теореме 1.4. для обозначения числа перестановок использовалась буква Р, что соответствует начальной букве французского слова «permutation», в переводе – перестановка.

Пример 1.8. Представитель торговой фирмы ежедневно просматривает 5 изданий, в которых исследуется спрос и предложение на определенные товары. Сколько существует способов просмотра, если выбор изданий случаен?

Решение. Каждый день все 5 изданий должны быть просмотрены, может меняться лишь порядок просмотра, поэтому число способов просмотра равно . ■

Пример 1.9. На полке стоят 7 учебников, 3 из которых по эконометрике. Сколько существует способов расстановки семи различных книг на полке так, чтобы 3 учебника по эконометрике стояли рядом?

Решение. Зафиксируем расположение трех учебников по эконометрике. Тогда остальные четыре учебника можно расставить на полке различными способами. В свою очередь учебники по эконометрике также можно переставить между собой способами. По правилу умножения число способов расстановки для семи книг равно .■

Во всех рассмотренных ранее примерах предполагалось, что элементы в одной перестановке все различны. Если допустить наличие одинаковых элементов в перестановке, то получим перестановки с повторениями. Так как перестановки – это частный случай размещений, то учитывая формулу (1.3) можно получить следующую формулу для числа перестановок с повторениями

(1.5)

Пример 1.10. Сколько различных чисел можно составить из трех цифр 3, 4, 5?

Решение. Применяя формулу (1.5), получим . Решим эту же задачу другим способом, без применения формулы (1.5).

Числа, состоящие из трех предложенных цифр можно разделить на три группы. В первую группу входят числа, в которых все цифры разные, например, 345, 534 и т.д. Очевидно, что их число равно 3!=6. Вторая группа состоит из чисел, в которых имеется две одинаковых цифры, например, с двумя цифрами 3 существует 6 различных чисел: 334, 343, 433, 335, 353, 533. Аналогично существует по 6 различных чисел с двумя цифрами 4 и 5. Следовательно, вторая группа состоит из 18 чисел. Наконец, третья группа составлена из чисел, в которых все три цифры одинаковы, т.е. 333, 444, 555. Таким образом, общее количество чисел равно 6+18+3=27.■

Для решения ряда задач бывает полезна формула, позволяющая найти число различных комбинаций из n элементов, среди которых есть конкретное число одинаковых элементов.

Пусть среди n элементов есть n₁ элементов одного вида, n₂ элементов второго вида и т.д. и n_k элементов k-го вида, тогда число перестановок из этих чисел равно

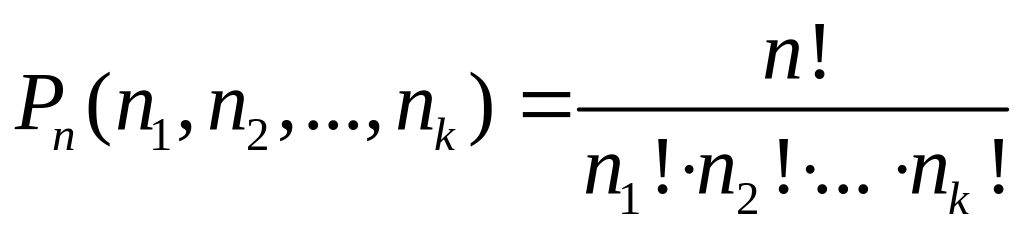(1.6)

где n₁+ n₂+…+ n_k= n.

Пример 1.11. Сколько существует различных шестизначных чисел, в которых цифра 1 повторяется два раза, цифра 3 один раз, цифра 5 – три раза?

Решение. Из условия задачи ясно, что n=6, n₁=2, n₂=1, n₃=3. По формуле (1.6) получим .■

Рассмотрим два различных размещения, которые состоят из одних и тех же элементов. Тогда они обязательно должны отличаться порядком расположения этих элементов. Однако часто бывает, что нет необходимости учитывать этот порядок, т.е. размещения, которые отличаются лишь расположением элементов считать равными. В этом случае полученные комбинации будут называться сочетаниями.