II. 3. Целочисленные задачи линейного программирования.

Многие задачи исследования операций из области экономики и управления описываются математическими моделями дискретного программирования (ДП). В этом разделе мы рассмотрим один частный случай задач дискретного программирования - целочисленные задачи линейного программирования (ЦЛП). Методы решения таких задач делятся на три основные группы: отсекающих плоскостей; ветвей и границ; случайного поиска и эвристические методы.

II. 3.1. Метод отсекающих плоскостей.

Этот метод именно и предназначен для решения частного случая задач дискретного программирования - ЦЛП.

Суть метода заключается в следующем. Временно, отбросив условия целочисленности переменных задачи, отыскивается оптимальный план прямым симплекс- методом. Если окажется, что он не удовлетворяет условиям целочисленности, то в задаче формируется дополнительное ограничение, называемое правильным отсечением, которому заведомо удовлетворяет любое целочисленное решение из ОДР рассматриваемой задачи и не удовлетворяет найденное оптимальное решение.

В общей постановке задача ЦЛП имеет вид¹:

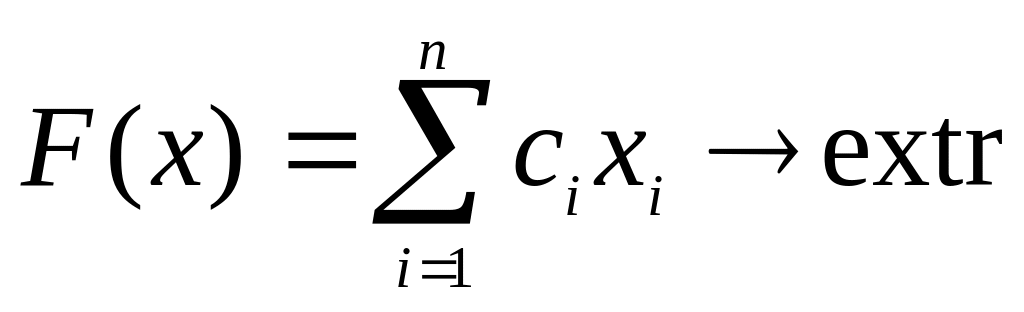
при ограничениях:

.

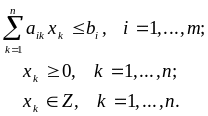1 Не нарушая общности рассуждений, для определенности будем предполагать, что все ограничения задачи - ограничения типа неравенств, и в системе ограничений рассматриваемой задачи они ориентированы.
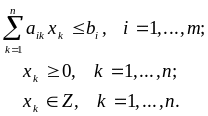