4.3. Степенные средние величины

Средняя величина — это обобщающая мера варьирующего признака, которая характеризует его уровень в расчете на единицу совокупности.

Средние величины рассчитываются на основе данных правильно организованного статистического наблюдения, а условиями их применения является наличие качественно однородной совокупности и достаточно большой ее объем.

Каждая средняя величина характеризует изучаемую совокупность по какому — либо одному признаку. Чтобы получить полное и всесто­роннее представление об изучаемой совокупности необходимо располагать системой средних величин.

В экономических исследованиях применяются две категории средних:

1) степенные средние;

2) структурные средние.

Название степенных средних связано с тем, что все они являются частным случаем степенной средней, определяемой по формуле

= (4.1)

где — индивидуальное значение признака;

— частота, соответствующая ;

— степень рассчитываемой средней величины.

К степенным средним относятся: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая.

4.3.1. Средняя арифметическая

Наиболее часто в экономико-статистических исследованиях используется средняя арифметическая ( ). Она применяется в тех случаях, когда объем изучаемого признака образуется как сумма значений отдельных единиц анализируемой совокупности. Средняя арифметическая может быть простой и взвешенной.

Простая средняя арифметическая рассчитывается по следующей формуле:

= (4.2)

где — индивидуальное значение признака (варианта);

n — объем совокупности (число единиц совокупности).

Простая средняя арифметическая применяется, как правило, при определении среднего уровня абсолютных величин при условии, что используемые при расчете данные не сгруппированы. Например, требуется определить средний стаж рабочих цеха по следующей информации.

Таблица 4.1 – Стаж рабочих цеха

№ рабочего	1	2	3	4	5	6	7	8	9	10	11	12
Стаж, лет	2	4	5	3	4	4	3	6	4	5	4	3

Используя формулу простой средней арифметической, получим размер среднего стажа рабочих цеха:

=

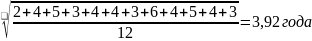
Если абсолютные данные сгруппированы и представлены в виде статистического ряда распределения, то в этом случае для решения аналогичной задачи используется средняя арифметическая взвешенная:

= (4.3)

Средняя арифметическая взвешенная используется при расчете среднего уровня относительных величии: средней производительности тру­да, себестоимости единицы продукции, рентабельности производства и других аналогичных показателей. Простая средняя арифметическая в этом случае, как правило, не используется.

При решении таких задач особое значение приобретает обоснование того показателя, который должен использования в качестве веса признака, средний уровень которого определяется. При выборе веса основополагающим моментом является сущность изучаемого показателя и аналитическая формула его расчета.

Рассмотрим схему выбора «веса» и самого расчета среднего уровня относительных экономических показателей на примере.

Пример 1. По данным табл. 4.2 определим удельный вес собственных средств в объеме инвестиций в среднем по акционерному обществу.

Таблица 4.2 – Доля собственных средств в инвестициях акционерного общества

Предприятие акционерного общества	Сумма инвестиций, млн. руб.	Удельный вес собственных средств в объеме инвестиций, %
№1	15,5	69,3
№2	40,0	57,4
№3	32,0	62,8

Запишем аналитическую формулу расчета показателя, средний уровень которого требуется определить:

Следовательно, при расчете удельною веса собственных средств в объеме инвестиций в целом по АО ( ), в знаменателе должна быть пока­зана сумма инвестиций в целом по всему акционерному обществу, то есть (15,5+40,0+32,0) млн. рублей. В числителе — величина собственных средств АО, используемых в качестве инвестиций. Величина этих средств как сумма их по отдельным предприятиям может быть определена поданным табл. 4.2 следующим образом:

(15,5x0,693 + 40,0x0,574 + 32,0 х 0,628) млн. рублей.

В результате:

= =

Таким образом, в данном случае вариантами ( ) являются удельные веса собственных средств в инвестициях по каждому предприятию, а весами — объемы инвестиций по каждому предприятию.

Пример 2. По данным табл. 4.3 определить рентабельность реализованной продукции в целом по предприятию.

Таблица 4.3 – Рентабельность отдельных видов реализованной продукции

Вид продукции	Затраты на производство и реализацию продукции, млн. руб.	Рентабельность реализованной продукции, %
А	5	8
Б	8	9,5

Рентабельность реализованной продукции определяется по формуле:

Прибыль предприятия от реализации всей продукции может быть рассчитана как сумма произведений затрат на рентабельность каждого вида продукции. В знаменателе должна быть представлена сумма затрат на производство всей продукции. В итоге средняя рентабельность:

Таким образом, в данной задаче вариантами ( ) являются показатели рентабельности каждого вида продукции, а весами — объем затрат на ее производство.

Из примеров видно, что в качестве весов в обоих случаях использовались величины, находящиеся в знаменателе формулы, по которой определяется показатель, средний уровень которого рассчитывается. Это явля­ется общим правилом.