5.2. Дисперсия альтернативного признака

Признак, для которою существует только два взаимоисключающих варианта значений, называется альтернативным. Например, годная и негодная (бракованная) продукция.

Эквивалентом такого признака можно считать переменную , которая принимает значение 1, когда обследуемая единица совокупности обладает изучаемым признаком или 0, когда не обладает.

Обозначим долю единиц, обладающих признаком (годная продукция) — р, а долю единиц, не облагающих признаком (бракованная продукция) – q.

Тогда (р + q)=1

По формуле средней арифметической взвешенной:

=

Таким образом, среднее значение альтернативного признака равно частости варианты, обладающей этим признаком.

Дисперсию альтернативного признака рассчитаем по формуле (5.6):

Заменив в этом выражении (1-р) на q, получим

Таким образом, дисперсия альтернативною признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих этим признаком. Предельное значение дисперсии альтернативного признака равно 0,25, когда p=q=0.5.

Пример. Известно, что качественные товары составили 85% всех отобранных при проверке товаров. Следовательно, на долю бракованных пришлось 15%.

В соответствии с выше записанными формулами:

=р=85%, а

Соответственно среднее квадратическое отклонение определится как

= 0,34.

5.3. Правило сложения дисперсий

Если изучаемую совокупность разбить на группы по какому-либо факторному признаку, то с помощью показателей дисперсии можно определить влияние этого фактора на колеблемость признака.

Для решения такой задачи необходимо исчислить три вида дисперсий: общую, межгрупповую и внутригрупповую.

Общая дисперсия 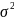характеризует вариацию признака по всей совокупности и учитывает влияние всех факторов, обусловливающих эту вариацию. Она рассчитывается по формулам (5.5) или (5.6).

Межгрупповая дисперсия отражает вариацию признака, возникающую под влиянием признака-фахтора, положенного в основание группировки. Она рассчитывается по формуле

. (5.10)

где — среднее значение изучаемого признака в выделенных группах; — среднее значение изучаемого признака по всей совокупности, — число единиц совокупности в каждой их выделенных групп.

Внутригрупповая (частная) дисперсия характеризует случайную вариацию в каждой из выделенных групп, то есть вариацию, не зависящую от признака-фактора, положенного в основание группировки. Она определяется по одной из формул:

. (5.11)

. (5.12)

Средняя из внутригрупповых дисперсий рассчитывается по формуле

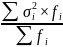= , (5.13)

где — внутригрупповая дисперсия в каждой из групп, — число единиц совокупности в каждой группе.

Согласно правилу сложения дисперсий, общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:

(5.14)

Рассмотрим алгоритм расчета определенных выше видов дисперсий на примере.

При изучении влияния квалификации (тарифного разряда) рабочих на уровень производительности труда были получены данные, представленные в таблице 5.2.

В этом примере результативный признак — среднечасовая выработка рабочих (Х), а факторный признак — квалификация рабочих (тарифный разряд). По факторному признаку все рабочие разделены на две группы.

Результативный признак варьирует под влиянием выделенного нами факторного признака и других неучтенных факторов. Степень влияния на результативный признак факторного признака характеризует межгрупповая дисперсия, а остальных факторов — внутригрупповая дисперсия. Определим каждую из них.

Таблица 5.2 – Распределение рабочих по среднечасовой выработке изделий

№ п/п	Рабочие 4 разряда				№ п/п		Рабочие 5 разряда
	Выработка (за час) изделий, штук			Выработка (за час) изделий, штук
1	2	3	4	5		6		7	8
1	7	–3	9	1		14		–1	1
2	9	–1	1	2		14		–1	1
3	9	–1	1	3		15		0	0
4	10	0	0	4		17		–2	4
5	12	2	4
6	13	3	9
∑	60	х	24	∑		60		х	6

1. Внутригрупповые дисперсии рассчитаем по формуле (5.11). Для расчета внутригрупповой дисперсии необходимо определить среднечасовую выработку рабочего по каждой из выделенных групп. Рассчитываем среднее значение выработки по каждой группе по формуле простой средней арифметической

По первой группе =60/6=10 шт; по второй =60/4=15 Внутригрупповая дисперсия (см. графы 4 и 8 табл. 5.2):

По первой группе =24/6=4; по второй группе =6/4= 1,5.

Внутригрупповые дисперсии характеризуют вариацию среднечасовой выработки под влиянием всех возможных факторов кроме одного — квалификации рабочих, поскольку внутри групп все рабочие имеют одинаковый тарифный разряд.

2. Средняя дисперсия из внутригрупповых дисперсий рассчитывается по формуле (5.13):

Эта дисперсия отражает вариацию среднечасовой выработки под влиянием всех действующих факторов, кроме квалификации рабочих.

3. Расчет межгрупповой дисперсии производим по формуле (5.10)

Для выполнения такого расчета, кроме среднечасовой выработки по каждой группе рабочих , требуется найти среднечасовую выработку по всей совокупности рабочих. Определим ее как средневзвешенную арифметическую из среднечасовой выработки, рассчитанной по каждой груп­пе (см. п.1 данного примера). По формуле средней арифметической взвешенной (4.3)

=

В соответствии с формулой (5.10)

Межгрупповая дисперсия характеризует вариацию признака, обусловленную различием квалификации рабочих.

4. Общую дисперсию исчисляем по формуле (5.11):

Общая дисперсия отражает влияние всех действующих факторов на вариацию среднечасовой выработки рабочих цеха.

5. Суммирование средней из внутригрупповых дисперсий и межгрупповой дисперсии дает, согласно формуле (5.14), общую дисперсию:

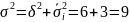
Для характеристики степени влияния факторного признака (в данном примере – квалификационного разряда) на результативный признак (в данном примере – среднечасовую выработку) в статистике используется эмпирический коэффициент детерминации, который рассчитывается как отношение межгрупповой дисперсии к общей дисперсии результативного признака η:

. (5.15)

Эмпирический коэффициент детерминации показывает долю межгрупповой дисперсии в общей дисперсии изучаемого признака. При отсутствии связи между группировочным и результативным признаком коэффициент равен нулю, а при функциональной связи между ними – единице.

В приведенном примере: η= 6/9=0,666. Это означает, что вариация производительности труда рабочих на 66,6% обусловлена различием их квалификации и на 33,4% — влиянием прочих факторов.

Квадратный корень из эмпирического коэффициента детерминации называется эмпирическим корреляционным отношением:

. (5.16)

Этот показатель, так же, как коэффициент детерминации, характеризует тесноту связи между факторным и результативным признаком и может принимать значение от 0 до 1. Чем ближе η к единице, тем значительнее связь изучаемых показателей.

В приведенном примере η = 0,812, что свидетельствует о тесной связи между производительностью труда рабочих и их квалификацией.

Для качественной оценки тесноты связи на основе эмпирического корреляционного отношения можно пользоваться соотношениями Чеддока:

η	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Сила связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная