
- •7. Берілген дифференциалдық теңдеуді шешіңіз:
- •Жазықтықтағы аналитикалық геометрия
- •1) Гиперболаның теңдеуін та-быңыз. 3
- •Сызықтармен шектел-ген фигураның ауданы неге тең:
- •Интеграл
- •18. Функциясы дербес туындыларын табыңыз:
- •6. Функциясы берілген. Нүктесінде дербес туындыларының қосындысының мәні:
- •Шек табу
- •Ықтималдықтар
Вектор
*![]() векторының коор-динаталарын
табу керек, егер
векторының коор-динаталарын
табу керек, егер
![]()
![]()
*![]() векторының ұзындығы тең:
векторының ұзындығы тең:
*![]() нүктесі арқы-лы
өтетін және
нүктесі арқы-лы
өтетін және
![]() векторына
перпенди-куляр
теңдеуі:
векторына
перпенди-куляр
теңдеуі:
*![]() және
және
![]() нүктелері берілген.
нүктелері берілген.
![]() векто-рының
ортогоналын табу керек.
векто-рының
ортогоналын табу керек.
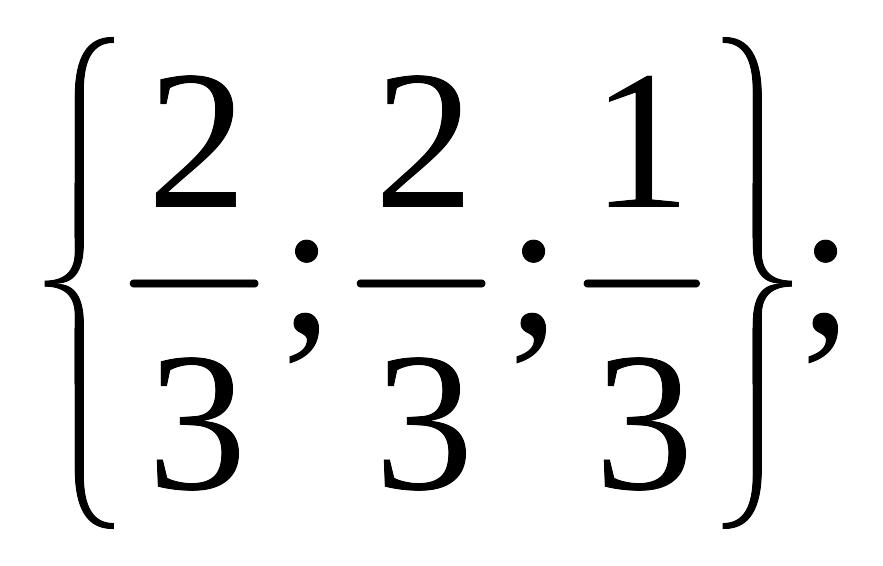
*![]() нүктелері берілген .
нүктелері берілген .
![]() векто-рының
абсциссасы тең: -3
векто-рының
абсциссасы тең: -3
*![]() векторының
ұзын-дығын табыңыз:
5
векторының
ұзын-дығын табыңыз:
5
*![]() және
және
![]() бе-рілген.
бе-рілген.
![]() векторының координаталарын табыңыз:
(4;0)
векторының координаталарын табыңыз:
(4;0)
*
векторы беріл-ген.
![]() векторының ұзынды-
векторының ұзынды-![]() ғын
табыңыз
ғын
табыңыз
![]()
*![]() векторы бе-рілген.
Осы вектордың коорди-наталарын
көрсетіңіз:
векторы бе-рілген.
Осы вектордың коорди-наталарын
көрсетіңіз:
![]()
*![]() и
и
![]() векторлары пер-пендикуляр
болғандағы
векторлары пер-пендикуляр
болғандағы
![]() -нің
мәнін табыңыз. -2
-нің
мәнін табыңыз. -2
*![]() және
және
![]() векторлары-ның скаляр көбейтіндісін
табу керек, егер
векторлары-ның скаляр көбейтіндісін
табу керек, егер
![]() және векторлар арасындағы бұрыш-тың
мәні
және векторлар арасындағы бұрыш-тың
мәні
![]() 3
3
*![]() векторы-ның
ұзындығы тең:
векторы-ның
ұзындығы тең:
![]()
*![]() векторының координаталарын табу керек,
егер
векторының координаталарын табу керек,
егер
![]()
![]()
*![]() вектордың ұзынды-ғын табыңыз: 5
вектордың ұзынды-ғын табыңыз: 5
*![]() векторлары сызықты тәуелді деп аталады,
егер бір мезгілде нөлге тең емес
векторлары сызықты тәуелді деп аталады,
егер бір мезгілде нөлге тең емес
![]() сандары та-былып, келесі қатынас
орын-далса:
сандары та-былып, келесі қатынас
орын-далса:
![]() *
*![]() ,
ал олардың арасындағы бұрыш
,
ал олардың арасындағы бұрыш
![]() тең болсын. Осы векторлардың скалярлық
көбейтііндісі тең:
тең болсын. Осы векторлардың скалярлық
көбейтііндісі тең:
![]()
*Бір жазықтықтың немесе паралель жазықтықтардың бойында жататын векторлар былай аталады: Компланар
*![]() және
және
![]() векторлары берілген. Осы векторлардың
аралдас көбейтіндісін табыңыз. -2
векторлары берілген. Осы векторлардың
аралдас көбейтіндісін табыңыз. -2
*![]() және
және
![]() векторларының арасындағы бұрыштың
коси-нусын табыңыз:
векторларының арасындағы бұрыштың
коси-нусын табыңыз:
![]()
*А![]() және В
және В![]() берілген.
берілген.
![]()
![]() векторының
координаталарын табыңыз :
векторының
координаталарын табыңыз :
![]()
*![]() және
және
![]() век-торларының арасындағы бұры-шы
век-торларының арасындағы бұры-шы
![]() .
.
![]() -ны
табың-ыз:
10
-ны
табың-ыз:
10![]()
*Екі
вектордың скаляр-лық көбейтіндісінің
формула-сы:
![]()
*![]() векторының ұзындығын табу керек, егер
векторының ұзындығын табу керек, егер
![]() болса. 5
болса. 5
*![]() нүктесі арқылы өтетін,
нүктесі арқылы өтетін,
![]() векторына перпендикуляр болатын түзу-дің
теңдеуі:
векторына перпендикуляр болатын түзу-дің
теңдеуі:
![]()
*![]() және
және
![]() векторлары берілген. Осы векторлардың
аралас көбейтіндісін табыңыз. -2
векторлары берілген. Осы векторлардың
аралас көбейтіндісін табыңыз. -2
*![]() және
және
![]() векторларының векторлық кө-бейтіндісін
та-быңыз
векторларының векторлық кө-бейтіндісін
та-быңыз
![]()
*![]() векторы бе-рілген.
Осы вектордың аппли-катасы
неге тең? 0
векторы бе-рілген.
Осы вектордың аппли-катасы
неге тең? 0
*Векторлардың компланар-лық шарты:
![]()
*![]() нүктесі арқылы өтетін және
нүктесі арқылы өтетін және
![]() векторы-на перпендикуляр болатын
жа-зықтықтың теңдеуін жа-зыңыз:
векторы-на перпендикуляр болатын
жа-зықтықтың теңдеуін жа-зыңыз:
![]()
![]() векторлары
берілсін. Өзара перпендикуляр
векторларды көрсетіңіз:
векторлары
берілсін. Өзара перпендикуляр
векторларды көрсетіңіз:
![]()
*Векторлардың
скалярлық көбейтіндісін табыңыз:
![]() 3
3
*
және
вектор-ларының скаляр көбейтіндісін
табу ке-рек, егер
![]() және
векторлардың арасын-дағы бұ-рыштың мәні
және
векторлардың арасын-дағы бұ-рыштың мәні
![]() .
3
.
3
*![]() векторларының векторлық кө-бейтіндісі
тең: (-7,21,-3)
векторларының векторлық кө-бейтіндісі
тең: (-7,21,-3)
*![]() және
және
![]() векторла-рының аралас көбейтіндісін
табыңыз. 33
векторла-рының аралас көбейтіндісін
табыңыз. 33
*![]() нүктесі арқылы өтетін және
нүктесі арқылы өтетін және
![]() век-торына перпендикуляр бола-тын
түзудің теңдеуін жазың-ыз:
век-торына перпендикуляр бола-тын
түзудің теңдеуін жазың-ыз:
![]()
*![]() векторы беріл-ген.
векторы беріл-ген.![]() векторы
мен
векторы
мен![]() осінің
арасындағы бұрыштың косину-сын табыңыз
осінің
арасындағы бұрыштың косину-сын табыңыз
![]()
*Векторлар арасындағы бұ-рыш-ты табыңыз
![]()
![]()
![]() векторларының
скалярлық кө-бейтіндісі: 4
векторларының
скалярлық кө-бейтіндісі: 4
*![]() және
және
![]() нүк-телері берілген.
нүк-телері берілген.
![]() бір-лік векторының координаталарын
көрсетіңіз
бір-лік векторының координаталарын
көрсетіңіз
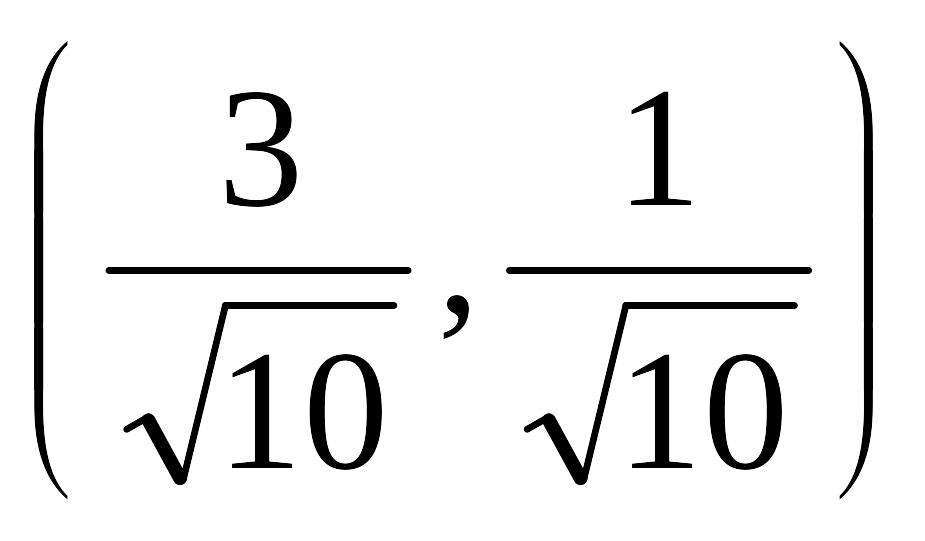
*![]() векторының бірлік вектор абсциссасы
тең :
векторының бірлік вектор абсциссасы
тең :
![]()
Дифференциал
*![]() дифференциал-дық
теңдеуінің реті
тең:
5.
дифференциал-дық
теңдеуінің реті
тең:
5.
*![]() сызық-тық
біртекті дифференциалдық теңдеуінің
жалпы шешімін та-быңыз.
сызық-тық
біртекті дифференциалдық теңдеуінің
жалпы шешімін та-быңыз.
![]()
![]()
*![]() дифференциал-дық теңдеуінің шеші-мін
та-быңыз:
дифференциал-дық теңдеуінің шеші-мін
та-быңыз:![]()
*![]() теңдеуіне
сәйкес біртекті сызықты тең-деудің
жалпы шешімін көрсе-тіңіз.
теңдеуіне
сәйкес біртекті сызықты тең-деудің
жалпы шешімін көрсе-тіңіз.
![]() .
.
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*Дифференциалдық теңдеу-дің жалпы шешімін табыңыз:
![]()
![]()
*![]() біртекті сызықты дифференциалдық
теңдеудің жалпы түбірін та-быңыз:
біртекті сызықты дифференциалдық
теңдеудің жалпы түбірін та-быңыз:
![]()
*Алғашқы
шарт
![]() қа-нағаттандыраты
қа-нағаттандыраты![]() дифференциалдық теңдеуінің шешуін
табыңыз:
дифференциалдық теңдеуінің шешуін
табыңыз:
![]()
*Бірінші
ретті
![]() дифференциалдық теңдеудің типін
анықтаңыз: Бірінші
ретті біртекті емес сызықты дифференциалдық
теңдеу.
дифференциалдық теңдеудің типін
анықтаңыз: Бірінші
ретті біртекті емес сызықты дифференциалдық
теңдеу.
*![]() теңдеуі-нің жалпы шешімін табыңыз.
теңдеуі-нің жалпы шешімін табыңыз.
![]() *
*![]() сызықтық біртекті дифференциалдық
тең-деуінің жалпы шешімін та-быңыз
сызықтық біртекті дифференциалдық
тең-деуінің жалпы шешімін та-быңыз![]()
*Теңдеуді
шешіңіз:
![]()
![]() *
*![]() дифференциал-дық теңдеуінің шешімін
та-быңыз
дифференциал-дық теңдеуінің шешімін
та-быңыз
![]()
*![]() дифференциал-дық теңдеуінің шешімін
та-быңыз
дифференциал-дық теңдеуінің шешімін
та-быңыз
![]()
*![]() ,
,
![]() Коши есебін шешіңіз:
Коши есебін шешіңіз:
![]()
*![]() функциясының то-
функциясының то-
лық дифференциалын табыңыз:
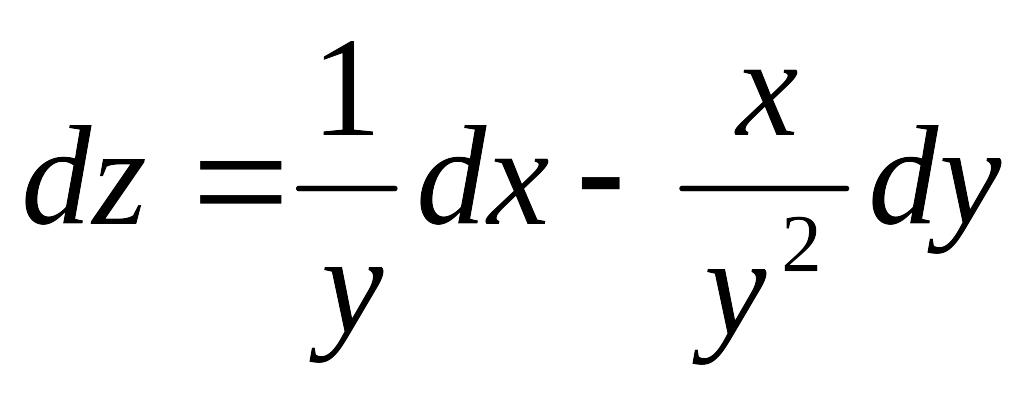
*![]() дифферен-циалдық теңдеуінің реті тең:
2
дифферен-циалдық теңдеуінің реті тең:
2
*![]() дифференциалдық
теңдеуінің реті тең:
3
дифференциалдық
теңдеуінің реті тең:
3
*![]() дифференциал-дық теңдеуінің ретін
төмендету үшін қолданылатын ауыстыру
дифференциал-дық теңдеуінің ретін
төмендету үшін қолданылатын ауыстыру
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:![]()
![]()
*1- ші
ретті дифференциал-дық теңдеуді
шешіңіз:
![]()
![]()
*1- ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*![]() тең-деуінің жалпы шешімін та-быңыз
тең-деуінің жалпы шешімін та-быңыз
![]()
*![]() дифференциал-дық теңдеуінің ретін
төмендету үшін, қажетті ауыстыруды
қолданамыз :
дифференциал-дық теңдеуінің ретін
төмендету үшін, қажетті ауыстыруды
қолданамыз :
![]()
![]()
*2-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті сызықтық диф-ференциалдық теңдеуді
көр-сетіңіз:
![]()
*Мына
функцияларының қайсысы
![]() теңдеуінің шешуі болады:
теңдеуінің шешуі болады:
![]()
*1-ші
ретті
![]() дифференциалдық теңдеуінің жалпы
шешімін табыңыз
дифференциалдық теңдеуінің жалпы
шешімін табыңыз
![]()
*2-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]() *
*![]() теңдеуінің кел-тірілген типтердің
қайсысына жататындығын анықтаңыздар:
теңдеуінің кел-тірілген типтердің
қайсысына жататындығын анықтаңыздар:
1-ші ретті біртекті емес сы-зықты дифферен/дық теңдеу.
*![]() теңдеуінің мінездемелік теңдеуін
құ-рыңыз:
теңдеуінің мінездемелік теңдеуін
құ-рыңыз:
![]()
*2-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*![]() -ші ретті диференциал-дық теңдеуді
анықтаңыз:
-ші ретті диференциал-дық теңдеуді
анықтаңыз:
![]() б)
б)
![]()
![]() б
б
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
15. 1-ші
ретті дифференциалдық теңдеуді шешіңіз:
![]()
![]()
*1-ші ретті дифференциал-
дық
теңдеуді шешіңіз:
![]()
![]()
*![]() функциясының толық дифференциалдық
фор-муласын көрсетіңіз.
функциясының толық дифференциалдық
фор-муласын көрсетіңіз.
![]() 7.
7.
![]() түрдегі бі-рінші ретті дифференциалдық
теңдеу берілсе, мұндағы
түрдегі бі-рінші ретті дифференциалдық
теңдеу берілсе, мұндағы
![]() және
және
![]() -
үзіліссіз функция-лар, оның атауы :
Сызықты
-
үзіліссіз функция-лар, оның атауы :
Сызықты
*Бірінші
ретті сызықтық теңдеу![]() келесі ауыстыру арқылы шешіледі:
келесі ауыстыру арқылы шешіледі:
![]()
*![]() дифференциалдық теңдеуінің реті тең:
3
дифференциалдық теңдеуінің реті тең:
3
*1- ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші ретті
дифференциалдық теңдеуді
шешіңіз:
![]()
![]()
*![]() дифференциалдық теңдеуін шешіңіз.
дифференциалдық теңдеуін шешіңіз.
![]()
*![]() дифференциал-дық теңдеуінің ретін
төмендету үшін қолданылатын ауыстыру:
дифференциал-дық теңдеуінің ретін
төмендету үшін қолданылатын ауыстыру:
![]()
*2-ші
ретті тұрақты коэффи-циентті сызықтық
біртекті тең-деудің фундаментальды
ше-шімдер жүйесінің
![]() және
және
![]() сипаттамалық теңдеудің әр-түрлі
түбірлері болған жағдай-да берілуі :
сипаттамалық теңдеудің әр-түрлі
түбірлері болған жағдай-да берілуі :
![]() ,
,
![]()
*![]() функциясының
то-лық
дифференциалын
табыңыз
функциясының
то-лық
дифференциалын
табыңыз
![]()
*![]() дифференциал-дық теңдеуінің реті тең:
2
дифференциал-дық теңдеуінің реті тең:
2
*![]() теңдеуін шешу үшін қолданылатын тәсіл:
теңдеуін шешу үшін қолданылатын тәсіл:
![]() ауыстыруын
жасау.
ауыстыруын
жасау.
*![]() теңдеуінің мінездемелік теңдеуін
құ-рыңыз:
теңдеуінің мінездемелік теңдеуін
құ-рыңыз:
![]() 22.
2-ші ретті дифференциалдық тең-деуді
шешіңіз:
22.
2-ші ретті дифференциалдық тең-деуді
шешіңіз:
![]()
![]()
*2-ші ретті дифференциал-
дық теңдеуді шешіңіз:
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеудің жалпы
түрі :
![]()
*![]() -ші
ретті дифференциал дегеніміз:
-ші
ретті дифференциал дегеніміз:
![]() -ші
ретті диф-ференциалдан, тағы дифферен-циал
алсақ
-ші
ретті диф-ференциалдан, тағы дифферен-циал
алсақ
*![]() дифференциал-дық теңдеуінің реті тең:
1
дифференциал-дық теңдеуінің реті тең:
1
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*Мына
дифференциалдық теңдеулерінің қайсысы
сызық-тық теңдеуге жатады:
1)
![]() 2)
2)
![]() 3)
3)
![]() 1,3
1,3
*2-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*![]() теңдеуі-нің жалпы шешімін табыңыз.
теңдеуі-нің жалпы шешімін табыңыз.
![]()
*![]() функциясы
функциясы
![]() теңдеуінің шешуі бола-тын
теңдеуінің шешуі бола-тын
![]() мәнін тап :
2
мәнін тап :
2
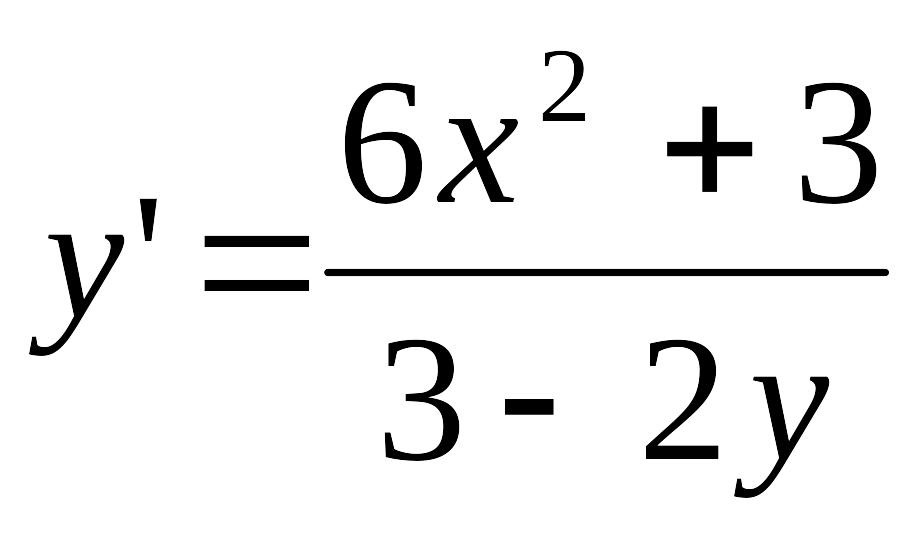 дифференциал-дық
теңдеуінің шешімін та-быңыз :
дифференциал-дық
теңдеуінің шешімін та-быңыз :
![]() *Берілген
дифференциалдық теңдеуді шешіңіз:
*Берілген
дифференциалдық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
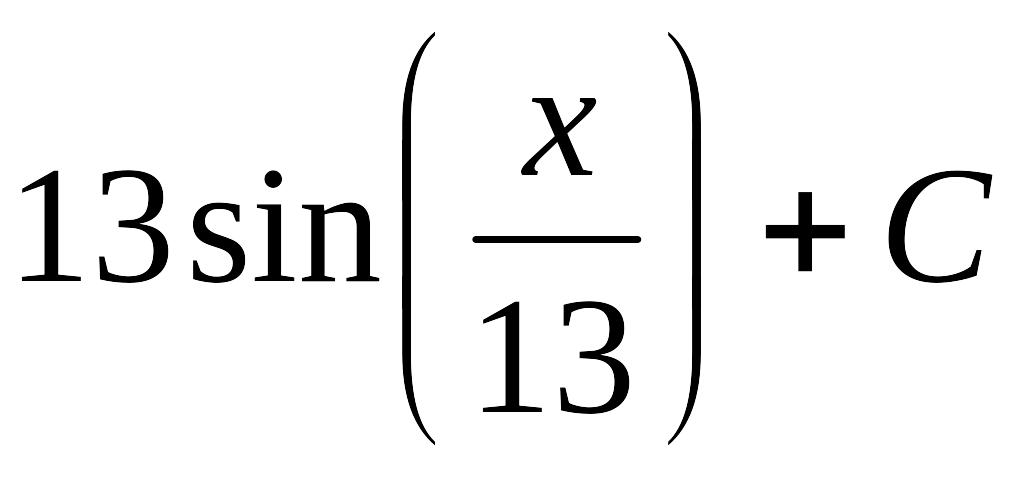
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*2-ші
ретті дифференциал дық теңдеуді шешіңіз:
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*Теңдеуді
шешіңіз:
![]()
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
*1-ші
ретті дифференциал-дық теңдеудің жалпы
шешімі-нің түрі:
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз :
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші ретті сызықтық диф-ференциалдық теңдеуді көр-сетіңіз : .
*1-ші ретті дифференциал-дық теңдеуді шешің:
![]()
![]()
*2-ші
ретті тұрақты коээф-фициенті
сызықтық біртекті теңдеудің фундаменталды
ше-шімдер
жүйесінің
![]() сипаттамалық теңдеуінің түбірлері
болған жағдайда берілуі:
сипаттамалық теңдеуінің түбірлері
болған жағдайда берілуі:
![]()
*2-ші ретті
дифференциал-дық теңдеуді
шешіңіз
![]() :
:
![]()
*2-ші ретті дифференциал-дық теңдеуді шешіңіз:
*1-ші ретті дифференциал-дық теңдеуді шешіңіз :
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз
:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз
:
![]()
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық
теңдеудің жалпы шешімі-нің
түрі :
![]()
*![]() теңдеуінің жалпы шешімін табыңыз
теңдеуінің жалпы шешімін табыңыз
![]()
*![]() сызықтық
сызықтық
біртекті дифференциалдық
теңдеуінің шешімін табыңыз
![]() *
*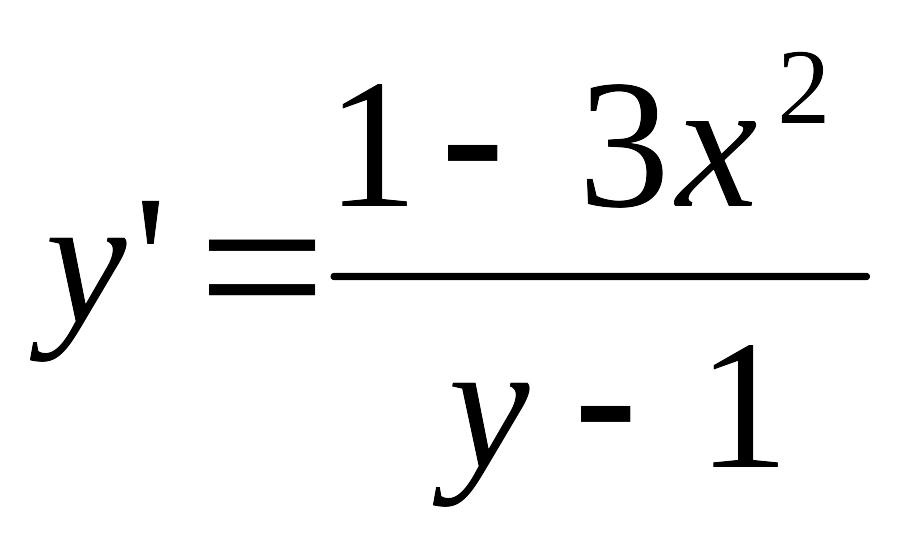 дифференциалдық теңдеуінің шешімін
табыңыз :
дифференциалдық теңдеуінің шешімін
табыңыз :
![]()
*![]() теңдеуіне қатыс-ты біртекті сызықты
теңдеуінің жалпы түбірін көрсетіңіз:
теңдеуіне қатыс-ты біртекті сызықты
теңдеуінің жалпы түбірін көрсетіңіз:![]()
*![]() функциясының дифференциалын табыңыз:
функциясының дифференциалын табыңыз:
![]()
*![]() функциясының дифференциалын табыңыз
:
функциясының дифференциалын табыңыз
:
![]()
*Дифференциалдық
теңдеу-дің жалпы шешімін табу керек:
![]()
![]()
*![]() біртекті диф-ференциалды теңдеудің
жалпы шешімі мынадай:
біртекті диф-ференциалды теңдеудің
жалпы шешімі мынадай:
![]()
*Дифференциалдық
теңдеу-дің жалпы шешімін табу керек:
![]()
![]()
* дифференциал-дық теңдеуін шешіңіз:
*Дифференциалдық
теңдеу-дің жалпы шешімін табу керек:
![]() .
.
![]()
*![]() функциясының то-лық
дифференциалын та-быңыз
:
функциясының то-лық
дифференциалын та-быңыз
:
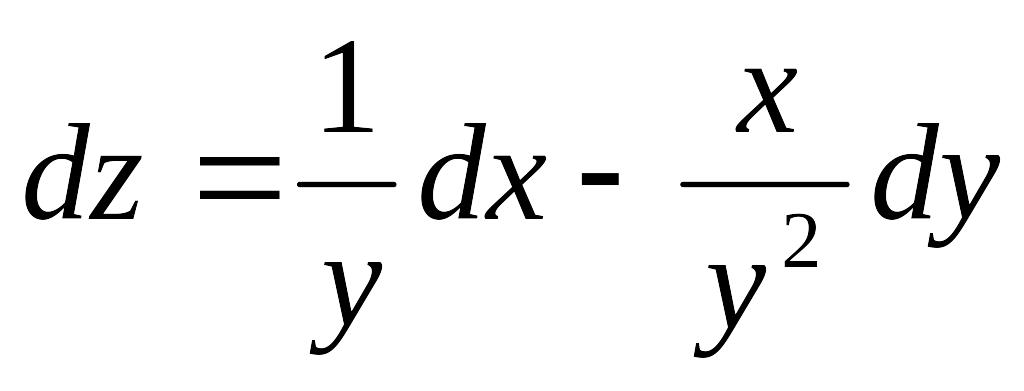
*![]() 1-ші
ретті диф-ференциалды
теңдеуді шешіңіз:
1-ші
ретті диф-ференциалды
теңдеуді шешіңіз:
![]()
*![]() функ-циясының стационарлық нүкте-лерін
табыңыз:
функ-циясының стационарлық нүкте-лерін
табыңыз:
![]()
*Дифференциалдық
теңдеу-дің
жалпы интегралын та-быңыз:
![]()
![]()
*1- ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1- ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1- ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1- ші ретті дифференциал-
дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*2- ші
ретті диференциал-дық теңдеуді ше-шіңіз:![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*![]() дифференциал-дық теңдеуінің жалпы
шешуін табыңыз:
дифференциал-дық теңдеуінің жалпы
шешуін табыңыз:
![]()
*Дифференциалдық теңдеу-
дің жалпы шешімін табыңыз
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*![]() характеристи-калық теңдеудің түбірлері
бе-рілген сызықтық біртектес тең-деуді
көрсетіңіз
характеристи-калық теңдеудің түбірлері
бе-рілген сызықтық біртектес тең-деуді
көрсетіңіз
![]()
*Мына
функциялардың қай-сысы
![]() функция-сының алғашқы функциясы болады?
функция-сының алғашқы функциясы болады?
![]()
*![]() дифференциалдық теңдеуін шешіңіз
дифференциалдық теңдеуін шешіңіз
![]()
*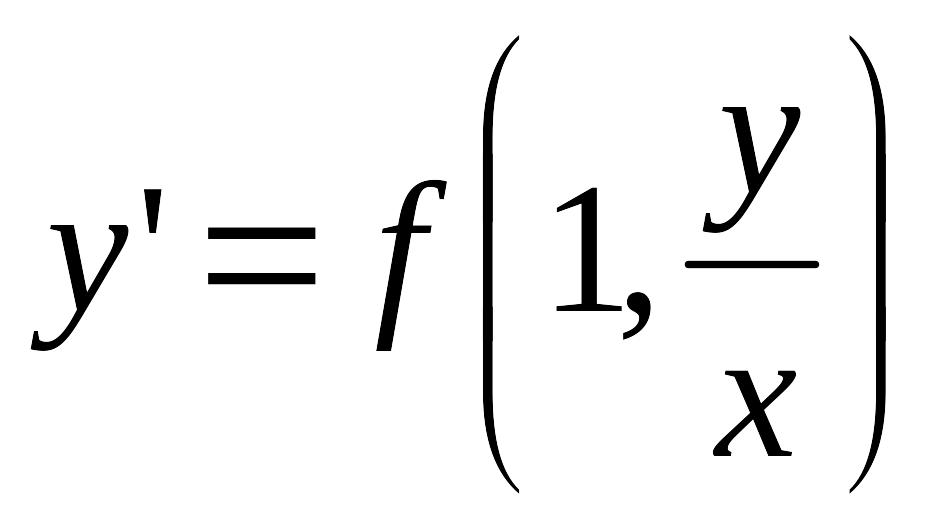 түріндегі диф-ференциалдық
теңдеудің атауы
Біртекті
түріндегі диф-ференциалдық
теңдеудің атауы
Біртекті
*1-ші ретті
дифференциалдық теңдеуді
шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
7. Берілген дифференциалдық теңдеуді шешіңіз:
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз.
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз.
![]()
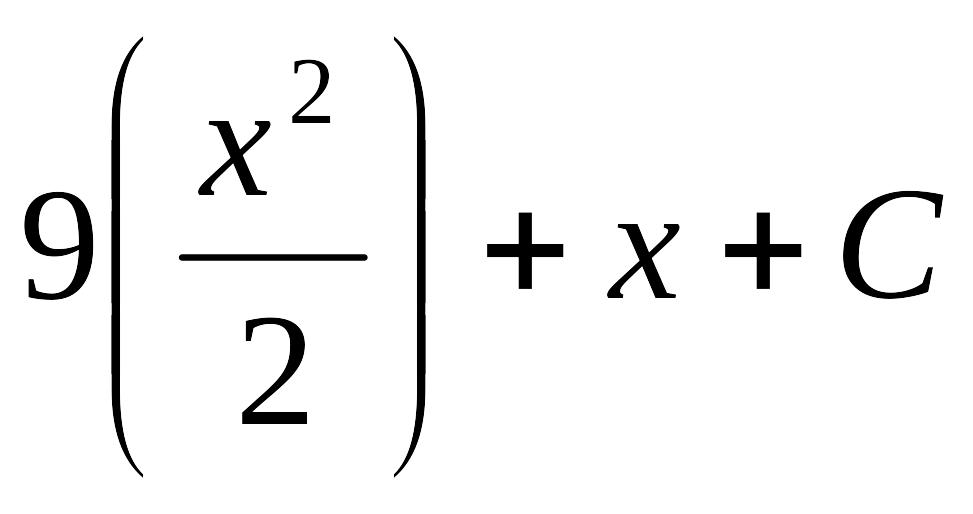
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз.
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*2-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*Теңдеуді
шешіңіз:
![]()
![]()
![]() функциясының толық дифференциалын
та-быңыз:
функциясының толық дифференциалын
та-быңыз:
![]() *
*![]() дифференциялдық теңдеуін шешіңіз:
дифференциялдық теңдеуін шешіңіз:![]() *1-ші ретті дифференциал-дық теңдеуі
шешіңіз:
*1-ші ретті дифференциал-дық теңдеуі
шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық
теңдеуі шешіңіз:
![]()
![]() +C
*1-ші
ретті дифференциал-дық
теңдеуі шешіңіз:
+C
*1-ші
ретті дифференциал-дық
теңдеуі шешіңіз:
![]()
![]()
*1-ші
ретті дифференциал-дық теңдеуі шешіңіз:
![]()
![]() 15.
15.
![]()
дифференциалдық теңдеудің
реті тең: 1
*1-ші
ретті дифференциал-дық теңдеуді шешіңз:
![]()
![]()
*Мына дифференциалдық теңдеулердің қайсысы сызықты теңдеуге жатады:
1)![]() 2)
2)![]() 3)
3)![]() 1,3
*Теңдеуді шешіңіз:
1,3
*Теңдеуді шешіңіз:
![]()
![]()
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
![]()
*1-ші
ретті дифференциал-дық теңдеуді шешіңіз:
![]()
![]()
*1-ші ретті дифференциал-дық теңдеуді шешіңіз:
*
![]()
дифференциал-дық теңдеуінің
жалпы
шешімін табыңыз![]()
*Берілгендердің арасындағы дифференциалдық теңдеу бола-тыны:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
3,4,5
* дифференциал-дық теңдеуін шешіңіз:
*![]() Коши есебін шешіңіз:
Коши есебін шешіңіз:
![]()
*![]() фундаменталды жүйелері бе-рілген
сызықтық біртектес тең-деуді көрсетіңіз:
фундаменталды жүйелері бе-рілген
сызықтық біртектес тең-деуді көрсетіңіз:![]()
*![]() дифферен-циалдық теңдеуінің реті тең:
4
дифферен-циалдық теңдеуінің реті тең:
4
*Мына
функциялардың қай-сысы
![]() теңдеуінің шешуі болады:
теңдеуінің шешуі болады:
![]()
*Дұрыс формуланы көр-сетіңіз:
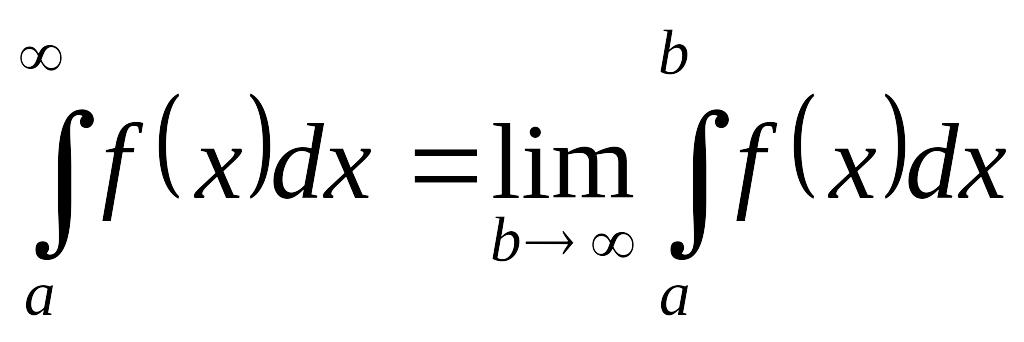 .
*
.
*![]() характеристикалық теңдеуі бе-рілген
сызықтық біртекті тең-деуді көрсетіңіз
характеристикалық теңдеуі бе-рілген
сызықтық біртекті тең-деуді көрсетіңіз
![]()
*![]() функциясының ал-ғашқы функциясы
функциясының ал-ғашқы функциясы
![]() болса, онда
функциясы-ның өзі неге тең?
болса, онда
функциясы-ның өзі неге тең?
![]()
*![]() .
Та-быңыз
.
Та-быңыз
![]()
![]() *
*![]() сызықтық функция-сы үшін
сызықтық функция-сы үшін
![]() аргументінің 1-ге өсуіне байланысты
аргументінің 1-ге өсуіне байланысты
![]() қаншаға өзгеретіндігін анықтау керек:
2
қаншаға өзгеретіндігін анықтау керек:
2
*![]() дифференциал-дық теңдеуінің реті тең:
1
дифференциал-дық теңдеуінің реті тең:
1
*![]() -ті
та-быңыз: ¼
-ті
та-быңыз: ¼
*![]() теңдеуінің мінездемелік теңдеуін
құ-рыңыз:
теңдеуінің мінездемелік теңдеуін
құ-рыңыз:
![]()
*![]() функциясының толық өсімшесінің түрі
қандай:
функциясының толық өсімшесінің түрі
қандай:
![]()
* тең-деуінің типін анықтаңыз:
Айнымалыларын бөліп алуға болатын теңдеу.
*![]() теңдеуінің типін анықтаңыз:
теңдеуінің типін анықтаңыз:
Айнымалыларын бөліп алуға болатын теңдеу
*![]() функция-сының біртектілік дәрежесін
анықтаңыз: 2
функция-сының біртектілік дәрежесін
анықтаңыз: 2
*![]() функциясының айнымалылары-на қатысты
біртектілік дәре-жесі тең: 3
функциясының айнымалылары-на қатысты
біртектілік дәре-жесі тең: 3
*![]() функ-циясының біртектілік дәреже-сін
анықтаңыз. 0
функ-циясының біртектілік дәреже-сін
анықтаңыз. 0
*![]() функ-циясының
функ-циясының
![]() -тегі
мәнін табыңыз
-тегі
мәнін табыңыз
![]()
*![]() функциясының айнымалылары-на қатысты
біртектілік дәрежесі неге тең?
3
функциясының айнымалылары-на қатысты
біртектілік дәрежесі неге тең?
3
*![]() Коши есебін шешіңіз:
Коши есебін шешіңіз:
![]()
*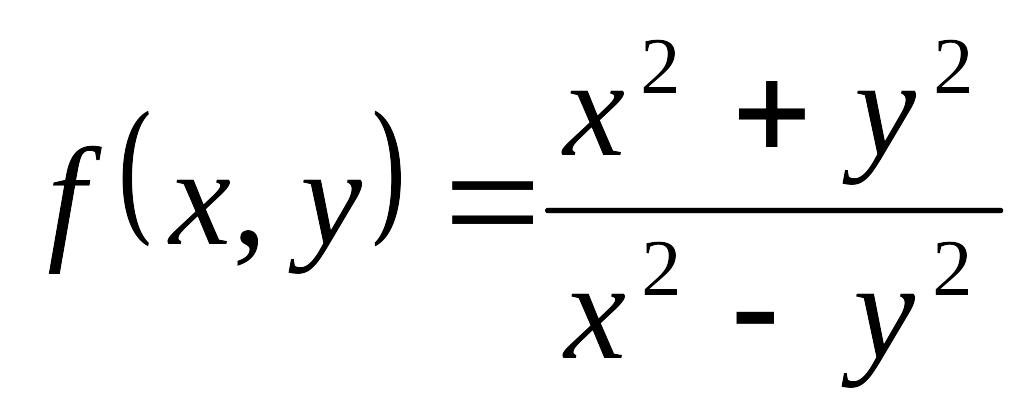
функциясының біртектілік дәрежесін анықтаңыз : 0
*![]() Коши есебін шешіңіз:
Коши есебін шешіңіз:
![]()
*![]() ,
,
![]() Коши есебін шешіңіз.
Коши есебін шешіңіз.
![]()
![]() функциясының
айнымалылары-на қатысты біртектілік
дәреже-сі тең:
3.
функциясының
айнымалылары-на қатысты біртектілік
дәреже-сі тең:
3.
*![]() функциясының айнымалылары-на қатысты
біртектілік дәрежесі тең:
3
функциясының айнымалылары-на қатысты
біртектілік дәрежесі тең:
3
*Үш белгісізі бар үш сызық-ты теңдеулер жүйесінің жалғыз шешімі болады, сонда тек қана сонда, егер бұл жүйенің анық-тауышы: нольге тең болмаса
