11.4. Выход темы в другие темы и дисциплины.

Тема «Формула Тейлора» имеет выход в другие темы курса «Высшей математики».

• функции двух переменных;

• ряды;

• аппроксимация эмпирических данных.

Тема «Кривизна кривой» имеет выход в другие дисциплины:

• сопротивление материалов;

• строительная механика;

• железобетонные конструкции;

• теория машин и механизмов;

• детали машин;

• теоретическая механика;

• теория пластичности (теория малых упругопластических деформаций А.А. Ильюшина);

• проектирование автомобильных и железных дорог.

11.5. Тест – контроль для самопроверки.

1. Справедливо ли равенство х² + 7х – 8 = 10 + 11 (х – 2) + (х – 2)?

А: да;

Б: нет.

2. Можно ли разложить по формуле Маклорена функцию

?

А: нет;

Б: да.

3. Записать разложение по формуле Маклорена функции у = е^х при п = 3.

А: ;

Б: ;

В: .

4. Записать остаточный член выше написанного разложения в ряд Маклорена функции у = е^х.

А: , 0    1;

Б: ;

В: .

5. Функцию f (х) = х³ разложить по формуле Тейлора по степеням разности (х – 1).

А: ;

Б: ;

В: х³ = 1 + 3 (х – 1) + 3 (х – 1)² + (х – 1)³.

6. Представить функцию f (х) = а^х (а  0) в виде многочлена третьей степени

относительно х.

А: а^х = 1 + х ln a + х² ln² a + х³ ln³ a + R₄ (х);

Б: ;

В: .

7. Чему равна кривизна прямой 2х – у + 7 = 0?

А: ;

Б: k = 2;

В: k = 0

8. Найти кривизну окружности х² + у² = 7.

А: ;

Б: ;

В: K = 0.

9. Если кривизна окружности равна 0,0625, то чему равен ее радиус?

А: R = 4;

Б: R = 0,25;

В: R = 16.

10. Как будет изменяться кривизна окружности, если радиус будет неограниченно возрастать?

А: K  ;

Б: K  0;

В: K  const

11. Чему будет равна кривизна кривой в точке перегиба?

А: k = const;

Б: k = ;

В: k = 0.

12. Написать формулу радиуса кривизны кривой у = е^х.

А: ;

Б: ;

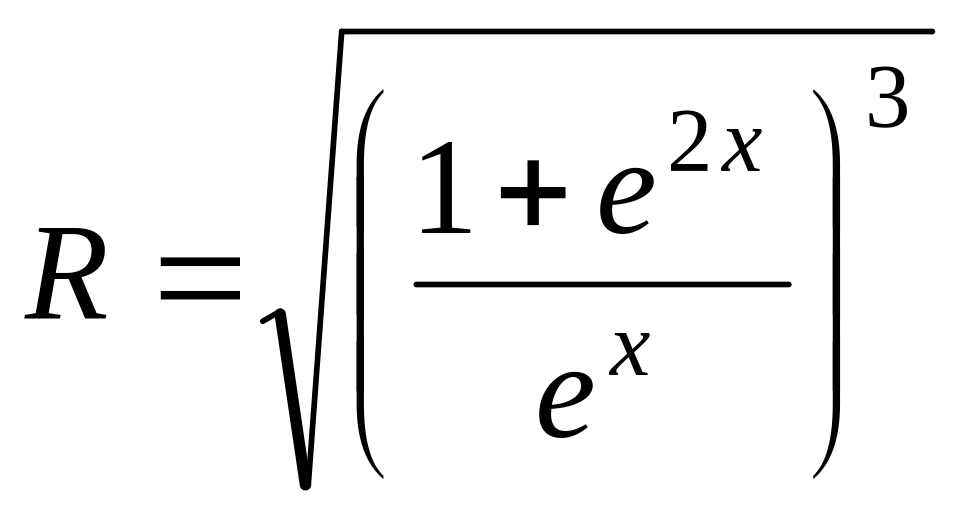В: .