§ 4. Применение формулы Маклорена при вычислении значений некоторых функций.

Пример. Приближенно вычислить sin 20^, положив k = 1 и оценить полученную ошибку, которая равна остаточному члену.

Решение. По условию задачи в разложении

ограничимся двумя членами

.

Оценим сделанную ошибку, которая равна остаточному члену

.

Следовательно, ошибка меньше, чем 0,001, т.е. sin 20^ = 0,343 с точностью до 0,001.

Задача. Вычислить число е с точностью до 0,0001.

Решение. В разложении

положим х = 1. Тогда

, 0    1.

Чтобы ошибка не превосходила 0,0001, надо определить п из условия, чтобы остаточный член, т.е.

,

был меньше 0,0001. Так как 0    1, то е^  3, и уже при п = 7 имеем

.

Итак, можно положить

= 2 + 0,5 + 0,16667 + 0,04167 + 0,00833 + 0,00139 + 0,00020 = 2,71826  2,7183.

Здесь слагаемые вычисляем с одним запасным знаком, чтобы не внести в подсчет дополнительной ошибки, и лишь результат округляем до нужного знака. Значение числа е с пятью знаками после запятой есть 2,71828…, что подтверждает правильность вычисления.

Применение формулы Маклорена при вычислении значений некоторых функций (11.4).

С помощью формулы Маклорена можно вычислить с любой заданной точностью значения тригонометрических функций y = sin x, y = cos x, показательной функции у = е^х, логарифмической функции у = ln x корня п-ой степени из числа.

11.4. Применение формулы Маклорена при вычислении значений некоторых функций (адрес файла Блок 4 ____ ). С помощью формулы Маклорена можно вычислить с любой заданной точностью значения тригонометрических функций y = sin x, y = cos x, показательной функции у = ех, логарифмической функции у = ln x, корня п-ой степени из числа. Вернитесь к тексту

§ 5. Средняя и истинная кривизна плоской кривой.

Степень искривленности, изогнутости кривой характеризует ее форму. Пусть задана кривая уравнением у = f (x) (Рис. 2).

Рис. 2.

На кривой возьмем две точки А и В. Угол поворота касательной при переходе от точки А к точке В обозначим через . Этот угол называется углом смежности дуги АВ. У двух дуг, имеющих одинаковую длину, больше изогнута та дуга, у которой угол смежности больше. Рассматривая дуги различной длины, невозможно оценить степень их искривленности только соответствующим углом

смежности. Отсюда следует, что полной характеристикой изогнутости кривой будет отношение угла смежности к длине соответствующей дуги.

Определение 1. Средней кривизной К_ср дуги называется отношение соответствующего угла смежности  к длине дуги

Н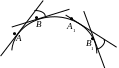 а рисунке 11.3 длины дуг и равны, но средняя кривизна дуги не равна средней кривизне дуги , более того, для одной и той же дуги вблизи различных ее точек кривая искривлена по разному (рис. 3).

Рис. 3.

Введем понятие кривизны кривой в данной точке.

Истинная кривизна плоской кривой (11.5).

Истинной кривизной или кривизной К_А линии в данной точке А называется предел средней кривизны дуги , когда длина этой дуги стремится к нулю.

(8)

11.5. Истинная кривизна плоской кривой (адрес файла Блок 4 ___ ). Истинной кривизной или кривизной КА линии в данной точке А называется предел средней кривизны дуги , когда длина этой дуги стремится к нулю. Вернитесь к тексту

§ 6. Вычисление кривизны линии, заданной уравнением у = f (х).

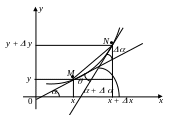
Найдем кривизну кривой у = f (х) в данной ее точке М (х; у) (рис. 4).

Рис. 4.

Возьмем на кривой отличную от М (х; у) точку N (х +  х, у +  у). Очевидно, что  =  , где    угол смежности дуги . Средняя кривизна дуги По определению (8) истинная кривизна в точке М (х; у). .

Для нахождения этого предела учтем следующие положения.

1. При  х  0 дробь 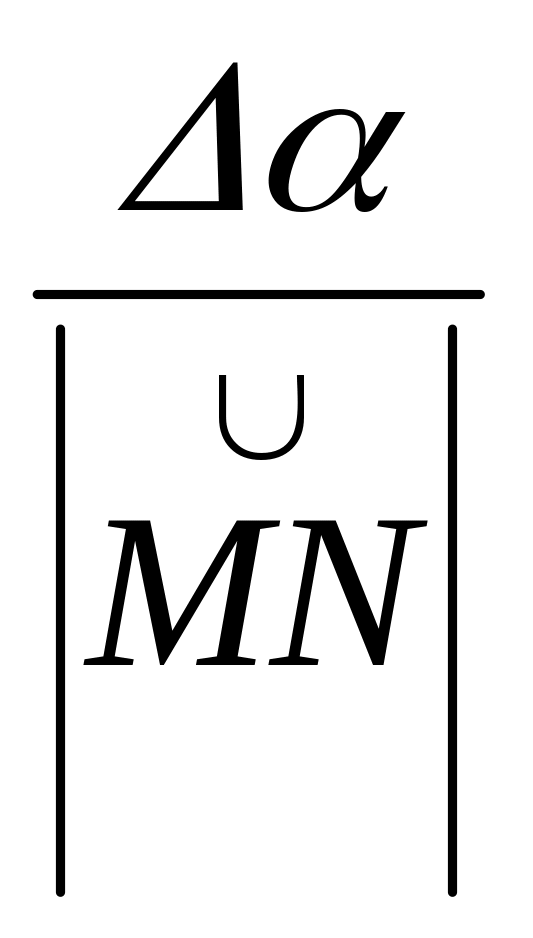есть неопределенность вида .

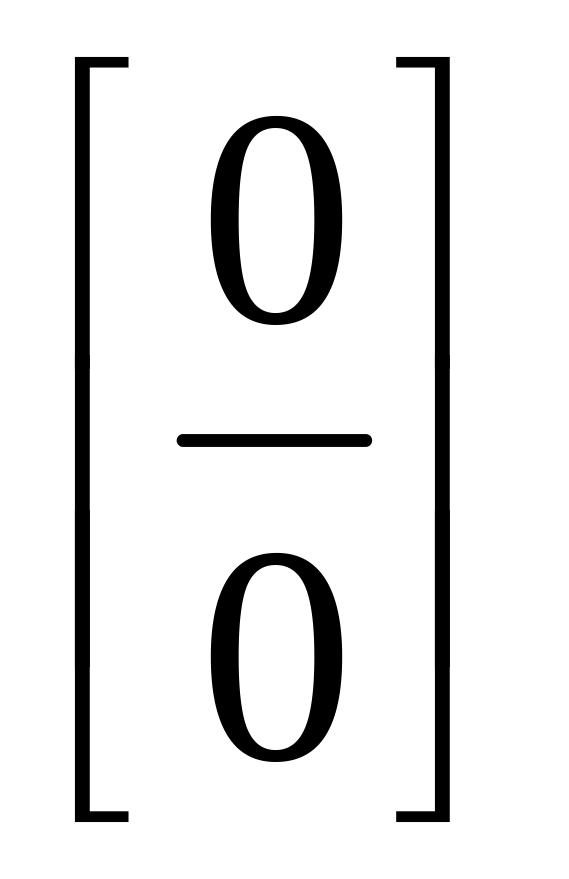2. При раскрытии таких неопределенностей можно заменить числитель и знаменатель дроби величинами им эквивалентными.

3. Бесконечно малая дуга эквивалентна своей хорде, то есть

.

Заменим на и учтем, что хорда есть расстояние между точками М (х, у) и

N (х +  х, у +  у). Значит

и

.

Это равенство можно переписать так:

.

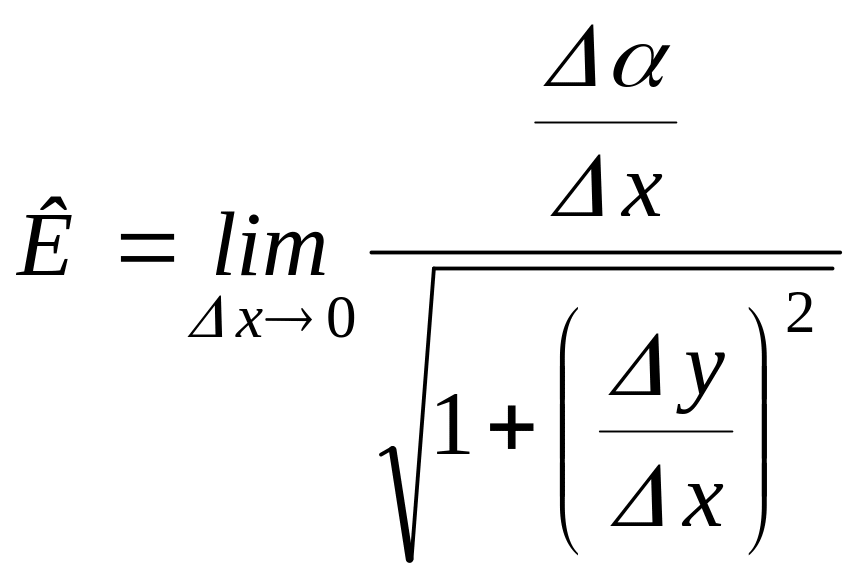Но, как известно,

, , тогда .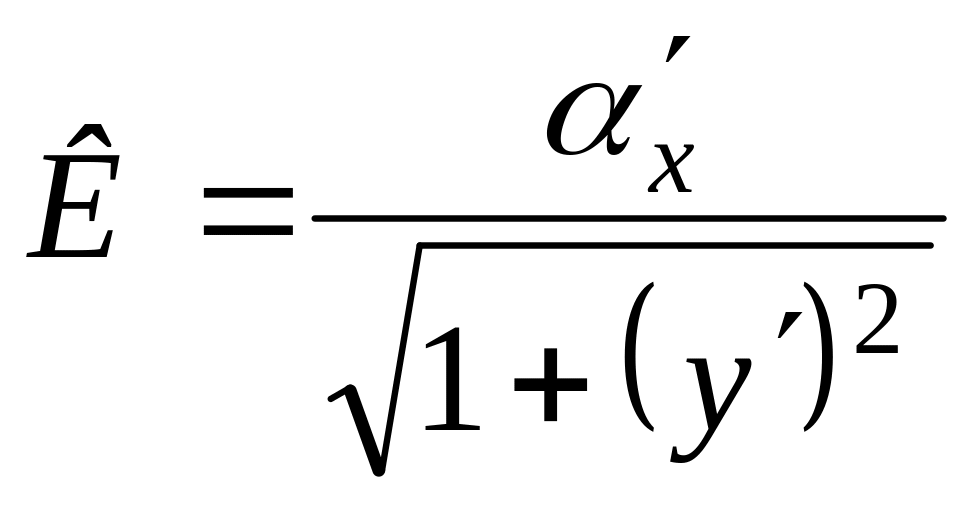

Вспомним геометрический смысл производной: у_х = tg , откуда  = arctg y_х и, дифференцируя это соотношение, получим

.

Таким образом, для кривизны получим формулу

.

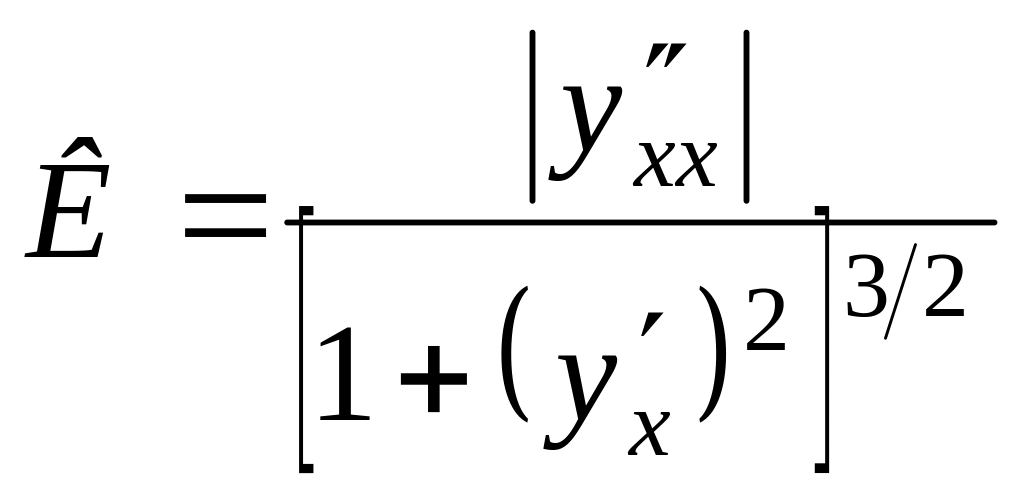Замечание 1. При вычислении кривизны кривой следует брать у_хх только по абсолютной величине и только арифметическое (то есть положительное) значение корня в знаменателе, так как кривизна линии по определению не может быть отрицательной.

Замечание 2. Обе производные у_х и у_хх должны вычисляться при абсциссе х той точки М, в которой ищется кривизна.

Замечание 3. Если у_х мало, то в практических расчетах значением у_х можно пренебречь и тогда К у_хх.

Вычисление кривизны линии, заданной уравнением у = f (х) (11.6).

Если кривая задана в декартовой системе координат уравнением вида у = f (х) и функция f (х) имеет непрерывную вторую производную, то кривизна кривой в любой ее точке М (х, у) вычисляется по формуле

(9)

11.6. Вычисление кривизны линии, заданной уравнением у = f (х) (адрес файла Блок 4 ___ ). Если кривая задана в декартовой системе координат уравнением вида у = f (х) и функция f (х) имеет непрерывную вторую производную, то кривизна кривой в любой ее точке М (х, у) вычисляется по формуле Вернитесь к тексту

Пример. 1) Найти кривизну прямой у = kx + b.

Решение. Найдем производные у_х и у_хх, у_х = k, у_хх = 0, следовательно К = 0 в любой точке прямой.

2) Найти кривизну окружности х² + у² = R².

Решение. Для определенности рассмотрим верхнюю полуокружность, в каждой точке которой у  0 и потому перед корнем надо выбрать знак «+», то есть

.

Тогда,

,

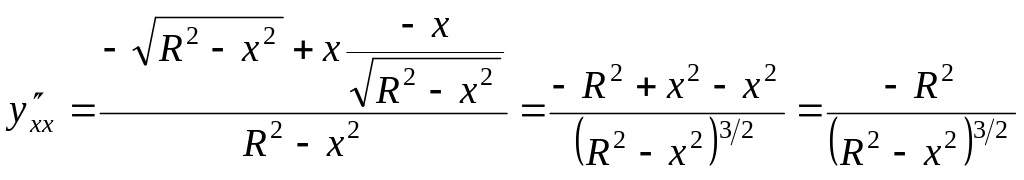
и кривизна

. ,

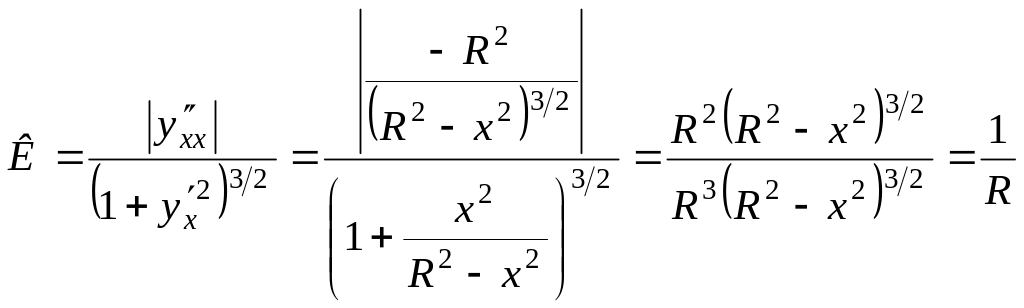то есть кривизна окружности во всех ее точках одинакова и равна единице, деленной на радиус окружности.

3) Найти кривизну синусоиды y = sin x.

Решение. у = соs х, у =  sin x, тогда

.

То обстоятельство, что К зависит от х, показывает, что кривизна синусоиды меняется от точки к точке. В точках перегиба у = 0. Касательная пересекает кривую.