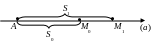ПМ. ДИФОП – 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ.

ПМ. ДИФОП – 1. Ключевые слова и понятия.

1. Задача о мгновенной скорости прямолинейного неравномерного движения.

2. Определение производной.

3. Геометрический смысл производной.

4. Односторонние производные функции в точке.

5. Непрерывность и дифференцируемость функции.

6. Производная постоянной.

7. Правило дифференцирования алгебраической суммы.

8. Правило дифференцирования произведения.

9. Правило дифференцирования частного.

1.1. Входная информация для самопроверки.

Приступая к изучению данной темы, Вам необходимо восстановить в памяти (или восполнить) знания из прошлых периодов обучения:

из темы «математический анализ»: теорема о функции, имеющей предел (5.13 ПМ – МА.5), теорема о пределе алгебраической суммы конечного числа функций (5.14 ПМ – МА.5); теорема о пределе произведения конечного числа функций (5.14 ПМ – МА.5).

1.2. Содержание темы

1.2.1. Структурно-логическая схема содержания темы

1.2.2. Тематическое содержание.

§ 1. Задача о мгновенной скорости прямолинейного неравномерного движения.

Исследование функций является одной из основных задач математического анализа.

Совершеннейшим аппаратом исследования является дифференциальное исчисление, создателями которого являются И. Ньютон (1642-1727) и Г.В. Лейбниц (1646-1716).

В основе дифференциального исчисления лежит понятие производной и дифференциала функции.

Рассмотрим задачу, решение которой подводит нас к понятию производной, а именно, задачу о скорости прямолинейного неравномерного движения.

Скоростью равномерного движения называется отношение пройденного пути за некоторый промежуток времени к этому промежутку времени (рис. 1).

Рис. 1.

, где S = f (t).

Путь материальная точка М движется по некоторой прямой (а) (в физическом рассмотрении точкой называется тело, размерами которого мы в данном рассмотрении пренебрегаем; в разных рассмотрениях точкой может считаться частица вещества или самолет, или даже небесное тело).

Точка М движется по прямой (а) слева направо, причем неравномерно, с переменной скоростью.

Пусть S, пройденный точкой М, отсчитываемый от некоторой точки А, связан с временем движения t формулой S = f (t).

S = f (t)  закон движения точки. Эта формула устанавливает функциональную зависимость пройденного пути от времени движения. Нужно определить скорость движения точки М в момент времени t = t₀. Пусть в момент времени t₀ движущаяся точка М занимала положение М₀, пройдя к этому моменту путь АМ₀ = S₀ (рис. 2)

Рис. 2.

По закону движения S0 = f (t0). Через промежуток времени t0 +  t точка М окажется в положении точки М1. Пройденный путь будет АМ1 = S1, где S1 = f (t0 +  t).

За промежуток времени  t точка М пройдет путь  S = f (t₀ +  t)  f (t₀).

Если взять отношение

,

то получим среднюю скорость неравномерного движения.

Но средняя скорость не характеризует состояние движения в определенный момент времени и потому в механике вводится важное понятие истинной скорости в данный момент времени, то есть мгновенной скорости.

Мгновенная скорость прямолинейного неравномерного движения (1.1).

Истинной скоростью точки в данный момент времени (мгновенной скоростью) называется предел средней скорости этой точки за бесконечно малый промежуток времени, стремящийся к данному моменту

(1)

1.1. Мгновенная скорость прямолинейного неравномерного движения (адрес файла Блок 4 __ ). Истинной скоростью точки в данный момент времени (мгновенной скоростью) называется предел средней скорости этой точки за бесконечно малый промежуток времени, стремящийся к данному моменту Вернитесь к тексту

Пример. Точка М движется по прямой по закону

S = 4t⁴ + 3t + 1.

Найти скорость V точки М в момент времени t = 5.

Решение. По условию задачи t₀ = 5, тогда

S (t₀) = S (5) = 4  5² + 3  5 + 1 = 116.

Дадим t₀ = 5 приращение  t, получим новый момент времени 5 +  t. По закону движения

S (t₀ +  t) = S (5 +  t) = 4 (5 +  t)² + 3 (5 +  t) + 1 =

=100 + 40  t + 4 ( t)² + 15 + 3 t + 1 = 1 ( t)² + 43  t + 116.

Тогда  S = S (5 +  t)  S (5) = 4 ( t)² + 43  t

.

Заметим, что скорость измеряется в единицах, зависящих от единиц длины и времени. Если считать в рассмотренном примере S означает расстояние в сантиметрах, а t – время в секундах, то полученный ответ означает, что S = 43 см/с.

Задача нахождения скорости неравномерного движения приводит к отысканию предела (1), но к такому же пределу приводит решение большого класса задач, связанных с изменением некоторого процесса.

Например: 1) Когда твердое тело вращается вокруг оси, то угол  поворота его есть функция времени t. Если за промежуток времени  t тело повернулось на угол  , то отношение

дает среднюю угловую скорость вращения за промежуток времени  t, а

(2)

дает угловую скорость вращения в момент времени t₀.

2) Обозначим через Q количество вещества, вступившее в химическую реакцию к моменту времени t₀. Тогда отношение

дает среднюю скорость химической реакции за промежуток времени  t, а

(3)

скорость химической реакции в момент времени t₀.

3) Обозначим через Q количество электричества (в кулонах), протекшее за время t₀ через поперечное сечение цепи. Силой тока J называется

 (4)

количество электричества, проходящее через поперечное сечение цепи в единицу времени.

Перечень таких задач можно продолжить и все они приводят нас к важнейшему понятию математического анализа – к понятию производной функции.