Получение оценок коэффициентов модели

П

(24)

араметры уравнения модели регрессии находятся методом наименьших квадратов из условия минимума величины ( y_i –f (x_i))² . Для линейной модели с n факторами при ПФЭ коэффициенты независимы и вычисляются по формуле b_j=

Т

(25)

.е. столбец соответствующего фактора умножается на столбец y_i и сумма почленных произведений делится на число опытов в матрице планирования (без учета параллельности). Аналогично вычисляются коэффициенты для взаимодействий факторов: b_jk=

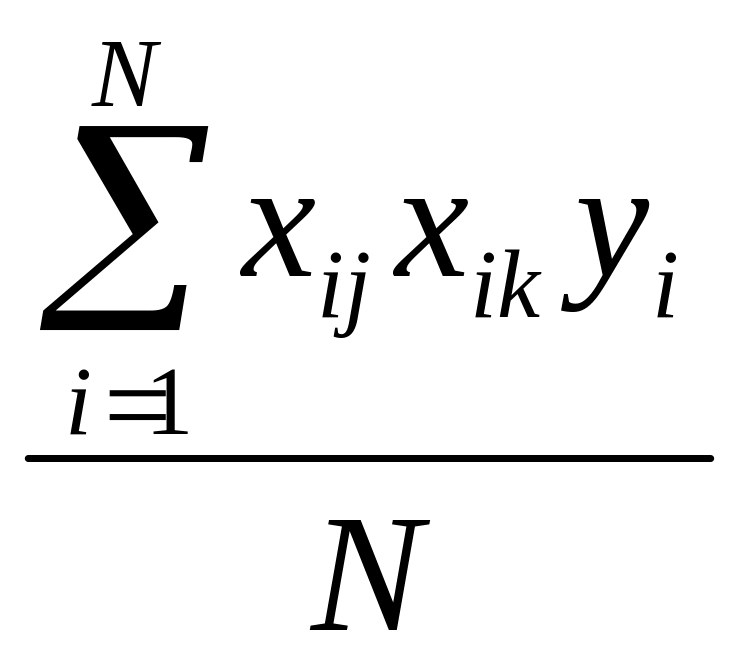
Проверка значимости коэффициентов математической модели

Проверка значимости каждого коэффициента основана на вычислении t-критерия Стьюдента. При использовании ПФЭ величины доверительного интервала для каждого из коэффициентов минимальны и равны (следствие ортогональности матрицы планирования). Для дробных реплик коэффициенты регрессии имеют большую дисперсию, чем коэффициенты, определенные по данным ПФЭ.

Сначала определются дисперсии коэффициента регрессии S_{b i} по формуле

S_bi = ,

(26)

з

(27)

атем вычисляют t=

и сравнивается с табличным при заданном уровне значимости и соответствующем числе степеней свободы. Проверке подлежат все коэффициенты. На основании результатов проверки проводится корректировка модели путем исключения незначимых факторов или эффектов взаимодействия.

Для ортогонального планирования все незначимые оценки могут быть приравнены нулю и соответствующие им члены уравнения регрессии отбрасываются без пересчета всех остальных оценок коэффициентов.

Незначимость оценок коэффициентов может быть обусловлена следующими причинами:

1)соответствующий фактор (или взаимодействие) не имеет функциональной связи с откликом Y;

2) эксперимент производится в окрестностях частного экстремума по соответствующему фактору;

3) интервал варьирования соответствующего фактора выбран малым;

4) дисперсия воспроизводимости S²_вос слишком велика, т.е. на фоне "шума" выделить влияние данного фактора невозможно.

Проверка адекватности математической модели

Проверка адекватности модели состоит в установлении возможности с помощью выбранной регрессионной модели объекта предсказывать с требуемой точностью значения выходной величины в некоторой области значений входной. Для этого прежде всего вычисляется оценка дисперсии адекватности

(28)

,

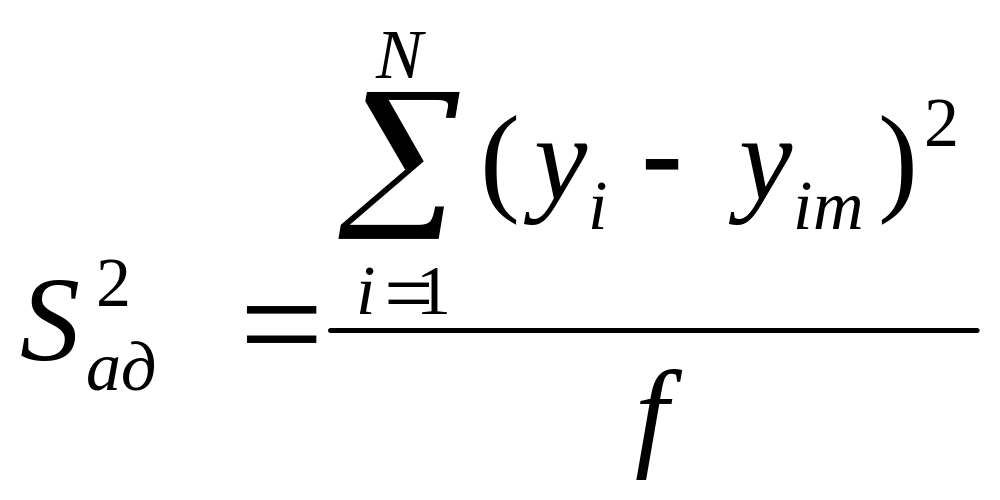
где у_i – реальное значение выходной величины, полученное в результате i-го опыта,

у_im – значение выходной величины, предсказанное в i-м опыте по полученной модели (для получения у_im необходимо подставить в модель значения факторов, предусмотренные матрицей планирования в i-м опыте, вычислить значение у_im по значениям факторов и коэффициентов модели);

f – число степеней свободы, равное числу различных опытов, результаты которых используются при подсчете коэффициентов модели, минус число определяемых коэффициентов.

Гипотеза об адекватности модели проверяется с помощью F-критерия:

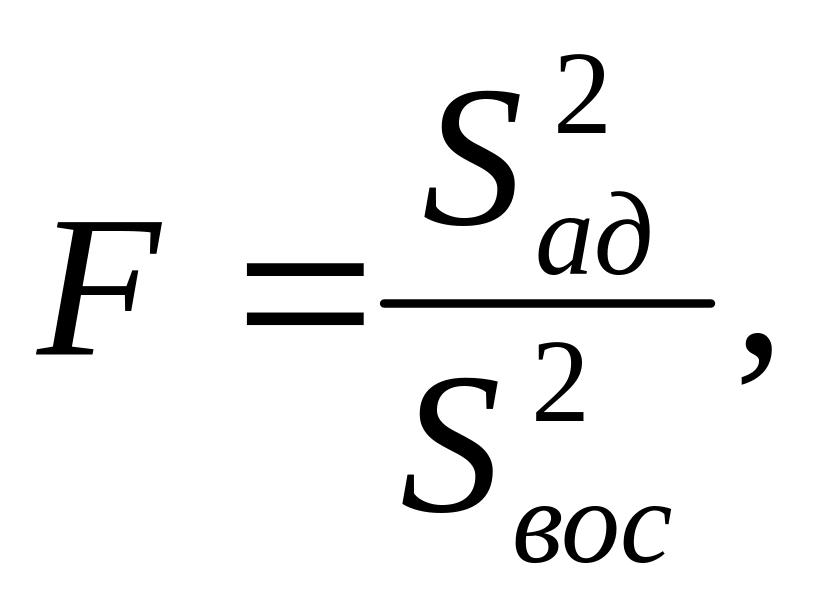(29)

где S²_вос – оценка дисперсии воспроизводимости со своим числом степеней свободы.

Модель считается адекватной, если рассчитанное значение F не превышает табличного. При несоблюдении этого условия проводится корректировка модели, вновь определяются коэффициенты и проверяется ее адекватность.

Решение о проведении дальнейших исследований принимается в зависимости от возможной ситуации.

1. Если коэффициенты регрессии значимы и линейная модель адекватна, то модель объекта можно считать построенной. При условии близости отклика к оптимальному значению f_min исследования можно закончить.

2. Если все коэффициенты регрессии незначимы (кроме b₀ ), а линейная модель адекватна, то необходимо расширить интервал варьирования или увеличить точность эксперимента (снизить S²_вос ) за счет большего числа параллельных опытов. Увеличение интервалов варьирования приводит к увеличению абсолютных величин коэффициентов регрессии.

3. Если линейная модель неадекватна, то это означает, что поверхность отклика не удается аппроксимировать плоскостью. В этом случае необходимо уменьшить интервалы варьирования, перенести нулевую точку варьирования или использовать более сложную модель - добавить взаимодействия факторов, т.е. перейти к нелинейным моделям. При сужении области экспериментирования необходимо помнить об ограничениях, накладываемых на минимальную величину Δx_j.

4. Если коэффициенты регрессии значимы, а план эксперимента является насыщенным, то адекватность проверить невозможно, т.к. в этом случае число степеней свободы, с которым определяется S²_ад , n-l=0 . Проверка возможна, если число коэффициентов модели меньше числа точек факторного пространства, в которых измерялся отклик. В этом случае можно провести дополнительные измерения в некоторой точке, например в x_o, тем самым увеличив n.