Найдите неизвестные углы треугольника abc

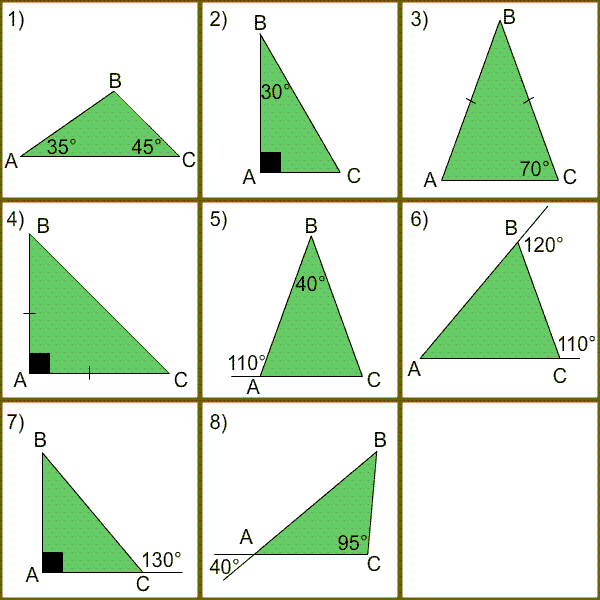
Подведение итогов урока

Что нового вы узнали на этом уроке?

В чем это новое заключается?

Где это применяется?

Постановка домашнего задания

1. Изучить доказательство теоремы по учебнику, выполнить запись теоремы в тетради.

2. Найти другие возможные способы доказательства.

Комментарий учителя к уроку

Эпиграфом урока я выбрала слова Л.Н.Толстого: «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью».

Очень часто обучение сводится к запоминанию и воспроизведению приёмов, действий, типовых способов решения заданий, к усвоению знаний и умений. Но требования современной ситуации таковы, что простого обладания суммой знаний недостаточно, необходима постоянная готовность к меняющимся условиям проблемной ситуации и умение рассмотреть её с разных точек зрения, найти наиболее рациональный способ решения.

Обучение математике, как правило, сводится к тому, что ребенка знакомят с определениями, правилами и формулами. Он решает типовые задачи, суть которых в том, чтобы в нужном месте применить нужный алгоритм. Развитие мышления происходит только у небольшой части детей, обладающих задатками для изучения математики. Большая же часть учеников просто заучивает формулировки и алгоритмы действий. При этом развивается память, но не мышление.

Использование методики, направленной на формирование метапредметных результатов в преподавании математики дает возможность развивать мышление у всех учеников. Суть такого подхода заключается в создании учителем особых условий, в которых дети могут самостоятельно, но под руководством учителя найти решение задачи. При этом педагог объясняет ребятам понимание сути задачи, построение эффективных моделей.

Помимо учебной цели урока - сформулировать и доказать одну из теорем геометрии «О сумме углов треугольника» - перед учителем ставятся и другие цели.

В метапредметном направлении – формирование представлений о значимости математики в развитии современного общества; создание условий для приобретения первоначального опыта математического моделирования.

В личностном направлении – развитие логического и критического мышления, культуры речи, способности к умственному эксперименту; формирование способности к преодолению мыслительных стереотипов.

Для достижения этих и других целей учащимся были предложены две практические работы.

Первая практическая работа подводит учащихся к предположению, которое в дальнейшем позволит сформулировать теорему. В ходе обсуждения этой работы формируется умение выдвигать гипотезы и понимать необходимость их проверки.

Вторая практическая работа направлена на поиск учащимися другого способа доказательства. Возможность использования иного пути учит их видеть различные стратегии в решении задач, а также позволяет самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.

Процесс доказательства теоремы был сконцентрирован на понимание учащимися сущности алгоритмических предписаний, что помогло действовать в соответствии с предложенным алгоритмом.

Работа на уроке учит ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию.

Обращение в процессе урока к интересным и важным фактам из истории математики дает возможность формировать представление о математической науке как сфере человеческой деятельности, о ее значимости для развития цивилизации.