Доказательство теоремы о сумме углов треугольника

Комментарий. Учащиеся открывают тетради и записывают тему урока «Сумма углов треугольника».

Работа над структурой теоремы

Учитель: Чтобы сформулировать теорему, ответьте на следующие вопросы:

• Какие треугольники использовались в процессе проведения измерений?

• Что известно из условия теоремы (что дано)?

• Что мы обнаружили при измерении?

• В чем состоит заключение теоремы (что надо доказать)?

• Попробуйте сформулировать теорему о сумме углов треугольника.

Построение чертежа и краткая запись теоремы

Комментарий. На этом этапе учащимся предлагается сделать чертеж и записать, что дано и что требуется доказать.

Построение чертежа и краткая запись теоремы.

Дано: Треугольник ABC.

டA, டB, டC - углы треугольника АВС. Доказать: டA + டB + டC = 180°.

Поиск доказательства теоремы

Комментарий. При поиске доказательства следует попытаться развернуть условие или заключение теоремы. В теореме о сумме углов треугольника попытки развернуть условие безнадежны, поэтому разумно заняться с учениками развертыванием заключения.

Учитель: В каких утверждениях говорится об углах, сумма величин которых равна 180°?

Ученик: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

Сумма смежных углов равна 180°.

Величина развернутого угла равна180°.

Учитель: Попробуем для доказательства использовать первое утверждение. В связи с этим необходимо построить две параллельные прямые и секущую, но необходимо это сделать так, чтобы наибольшее количество углов треугольника стали внутренними или входили в них. Как можно этого добиться?

Поиск доказательства теоремы

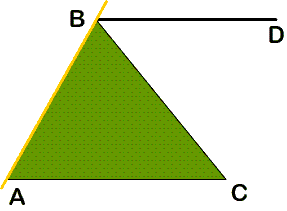
Ученик: Провести через одну из вершин треугольника прямую параллельную другой стороне, тогда боковая сторона будет являться секущей. Например, через вершину В. Строим часть прямой, луч BD.

Учитель: Назовите образовавшиеся при этих прямых и секущей односторонние углы.

Ученик: Углы DBA и ВАС.

Учитель: Сумма каких углов будет равна 180°?

Ученик: டDBA и டBAC.

Учитель: Что можно сказать о величине угла ABD?

Ученик: Его величина равна сумме величин углов ABC и СВК.

Учитель: Какого утверждения нам не хватает, чтобы доказать теорему?

Ученик: டDBC = டACB.

Учитель: Какие это углы?

Ученик: Накрест лежащие углы.

Учитель: На основании чего мы можем утверждать, что они равны?

Ученик: По свойству накрест лежащих углов при параллельных прямых и секущей.

Комментарий. В результате поиска доказательства составляется план доказательства теоремы:

План доказательства теоремы

1.Через одну из вершин треугольника провести прямую (луч), параллельную противолежащей стороне.

2.Доказать равенство внутренних накрест лежащих углов.

3.Записать сумму внутренних односторонних углов и выразить их через углы треугольника.

Доказательство теоремы и его запись

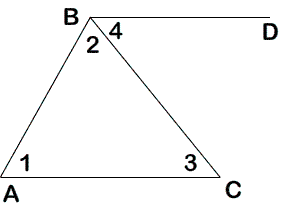
1. Проведем BD || АС (аксиома параллельных прямых).

2. ட3 = ட4 (так как это накрест лежащие углы при BD || АС и секущей ВС).

3. டА + டАВD = 180° (так как это односторонние углы при BD || АС и секущей АВ).

4. டА + டАВD = ட1 + (ட2 + ட4) = ட1 + ட2 + ட3 = 180°, что и требовалось доказать.

Закрепление формулировки теоремы и ее доказательства

Комментарий. Для усвоения формулировки теоремы учащимся предлагается выполнить следующие задания:

1. Сформулируйте теорему, которую мы только что доказали.

2. Выделите условие и заключение теоремы.

3. К каким фигурам применима теорема?

Применение знаний, формирование умений и навыков.

Учитель: После доказательства теоремы вернемся к задаче, которая явилась мотивацией для изучения теоремы.

Задача

Дано: Треугольник ABC, угол A = 50°, угол B = 100°, Найти: угол C.

Решение: டA + டB + டC = 180° (по теореме о сумме углов треугольника) ⇒ டC = 180° - (டA + டB) = 180° - (50° + 100°) = 30°.Ответ: 30°.

Ученик: Сумма углов в треугольнике практическим путем была установлена еще в Древнем Египте. В первой книге «Начал» Евклид излагает доказательство теоремы о сумме углов треугольника, которое легко понять при помощи чертежа. Великий древнегреческий философ Аристотель в своей «Метафизике» упоминает об этом предложении как известном ему.

Учитель: Мы рассмотрели только один из способов доказательства теоремы. Но ее история уходит в глубь веков и имеет не единственный путь доказательства. Сейчас вам предстоит найти еще один из них.

Практическая работа №2 (работа в парах)

Комментарий. Каждая пара получает карточку с чертежом треугольника, а также шаблон треугольника (равного треугольнику, изображенному на чертеже). Все пары получают задание найти новый способ доказательства теоремы, основываясь на утверждении, что величина развернутого угла равна 180º. Для выполнения работы ученикам предлагается отрезать углы треугольника (шаблона) и, используя чертеж, изображенный на карточке, составить из них развернутый угол.

Учитель сканирует одну из работ на экран. Ученик описывает доказательство.

1. Проведем BD || АС (аксиома параллельных прямых).

2. ட1 = ட4 (так как это накрест лежащие углы при BD || АС и секущей AB).

3. ட3 = ட5 (так как это накрест лежащие углы при BD || АС и секущей BC).

4. டА + டB +டC = ட1 + ட2 + ட3= ட4 + ட2 + ட5 = 180°, что и требовалось доказать.

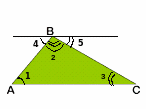
Учитель: Мы нашли еще один способ доказательства теоремы и наша гипотеза о том, что сумма углов в треугольнике равна 180°, подтверждается.

Комментарий. Учащиеся получают карточки с задачами, которые проверяют доказанную теорему. Решают задачи в парах, затем обсуждение происходит у доски.