Планы-конспекты уроков Математика

Урок по геометрии в 7 классе

Учитель: Демянчик Светлана Павловна

Тема урока: Сумма углов треугольника.

Эпиграф урока: «Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью». Л. Н Толстой.

Тип урока: урок изучения нового материала.

Цели урока:

Образовательные: доказать теорему о сумме углов треугольника;

Метапредметные: совершенствование умений осознанно проводить такие приемы мышления как сравнение, обобщение и систематизация.

Личностные: развитие логического и критического мышления, культуры речи, способности к умственному эксперименту.

Структура урока.

1. Актуализация знаний.

   1. Мобилизующее начало урока.

   2. Постановка проблемной задачи с целью мотивации изучения нового материала.

   3. Постановка учебной задачи.

2. Формирование новых знаний и способов действий.

   1. Практическая работа №1 «Сумма углов треугольника. Измерение углов треугольника»

   2. Доказательство теоремы о сумме углов треугольника первым способом.

   3. Практическая работа №2 «Сумма углов треугольника. Поиск доказательства теоремы»

   4. Доказательство теоремы о сумме углов треугольника вторым способом.

3. Применение знаний, формирование умений и навыков.

   1. Решение проблемной задачи.

   2. Решение задач по готовым чертежам.

   3. Подведение итогов урока.

   4. Постановка домашнего задания.

План урока:

1. Экспериментальным путем установить и выдвинуть гипотезу

о сумме углов любого треугольника.

2. Доказать это предположение.

3. Закрепить установленный факт.

Учитель: Треугольник – одна из основных фигур геометрии. Изучив его виды, свойства, мы сможем открыть свойства других геометрических фигур на плоскости и в пространстве. Если я задам вам вопрос: «Чему равна сумма углов треугольника?», думаю, вы легко ответите. Наша цель сегодня не только ответить на этот вопрос, а выполняя практические задания и приводя логические рассуждения, доказать теорему о сумме углов треугольника. Приведу слова Л.Н. Толстого: «Знание только тогда знание, когда оно приобретено усилием мысли, а не памятью».

Учитель: На предыдущем уроке мы выполнили практическую работу и сделали обоснование того факта, что треугольник не всегда существует. Его существование зависит от величин углов. Как можно узнать, чему равна сумма углов треугольника?

Ученик: Практически — измерением, теоретически — рассуждением.

Рассмотрим такую задачу.

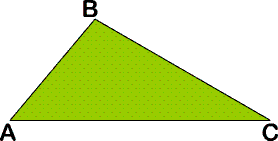
Задача

Дано: Треугольник ABC, угол A = 50°, угол B = 100°, Найти: угол C.

Учитель: Как вы считаете, можно ли решить эту задачу?

Ученик: Да.

Учитель: Сколько решений имеет эта задача?

Ученик: Одно.

Учитель: При каком условии задача будет иметь единственное решение?

Ученик: Задача имеет единственное решение, если сумма углов любого треугольника величина постоянная.

Учитель: То есть, для решения задачи надо знать величину суммы углов треугольника.

Практическая работа №1 (работа в парах)

Комментарий. Каждая группа получает карточки. Ученики, работая в парах, измеряют углы в различных треугольниках. Фиксируют результаты измерений.

Учитель: Почему мы пока не можем утверждать, что сумма углов абсолютно любого треугольника равна 180°?

Ученик: Нельзя выполнить ни абсолютно точных построений, ни произвести абсолютно точного измерения, даже на компьютере. Утверждение, что сумма углов треугольника равна 180°, относится только к рассмотренным нами треугольникам. Мы ничего не можем сказать о других треугольниках, так как их углы мы не измеряли.

Учитель: Правильнее было бы сказать: рассмотренные нами треугольники имеют сумму углов, приблизительно равную 180°. Чтобы убедиться в том, что сумма углов треугольника точно равна 180° и при этом для любых треугольников, нам надо еще провести соответствующие рассуждения, то есть доказать справедливость утверждения, подсказанного нам опытом.