Сканирование с постоянным шагом
Каждая переменная получает свое приращение Δx1 и Δx2 . При фиксированном значении одной из переменных(в данном случае х2) рассчитывается значение целевой функции в ряде точек отстоящих друг от друга на расстоянии Δx1. После того, как пройден весь интервал по переменной х1 , переменная х2 получает свое приращение и снова рассчитываются значения целевой фукнции по переменной х1.
Недостаток – большой объем вычислений. С целью уменьшения затрат на поиск используют метод сканирования с переменным шагом, для этого значения Δx принимаются заведомо большими, чем при поиске с постоянным шагом.
При таком сканировании определяется область расположения экстремума. Шаг поиска(Δx) уменьшается, и сканирование с уменьшенным шагом происходит только в найденной области.
Применение данного метода позволяет на несколько порядков уменьшить вычислительные затраты.
Сканирование по спирали
На каждое вычисление значения функции увеличивается шаг по каждой из переменных.
Симплексный метод
Основная идея метода заключается в том, что по найденным значениям целевой функции в вершинах многогранника, называемого симплексом, определяется направление движения экстремума. При этом под симплексом в n-мерном пространстве независимых переменных, понимается геометрическая фигура, имеющая n+1 вершину.
Одним из важнейших свойств симплекса является то, что против каждой из его вершин находится только одна грань, на которой может быть построен новый симплекс, отличающийся от исходного расположением новой вершины.
Рассмотрим основную стратегию метода на примере функции двух переменных:
По известному значению целевой функции в исходной точке S1 определяются вершины исходного сиплекса(S1, S2, S3) По любому из правил построения треугольника. Далее определяется вершина, в которой функция принимает наихудшее значение(S1). Построение нового симплекса происходит путем замены вершины S1 на вершину S4 , для этого вершина S1 отражается симметрично центру противоположной грани на расстояние, равное расстоянию от S1 до центра. В новом симплексе процедура повторяется( S2 заменяется на S5).
На промежуточных этапах поиска может возникнуть этап зацикливания, в этом случае уменьшается расстояние, на которое переносится новая вершина.
Для многомерного поиска вычислительный алгоритм может быть представлен следующим образом:
….
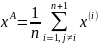ХA – координаты центра противоположной грани
Суммирование осуществляется по векторам, образующих противоположную грань.
Вектор U, характеризующий расстояние от центра до наихудшей вершины может быть определен по правилу:
U=x(A)-x(j)
И тогда координаты новой вершины могут быть определены по следующему условию:
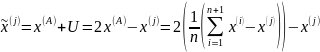
Целесообразнее всего при поиске использовать правильные фигуры. В этом случае направление движения к экстремуму совпадает с направлением градиента.