Метод с использование чисел Фибоначчи
Основная идея метода
заключается в постепенном изменении
шага поиска, связанному с выборкой чисел
Фибоначчи в убывающей последовательности.
На первом этапе поиска определяется
вспомогательное число N
по правилу: N=
,
где Δ – требуемая абсолютная
точность нахождения экстремума.
На втором этапе определяется число Фибоначчи, максимально приближенное к найденному значению N: Fs-1<=N<=Fs
На следующем этапе определяется максимальный шаг поиска:
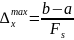
Находится следующая точка, в которой должна быть вычислена целевая функция(с любого конца отрезка). x1=a+ΔxFs-1
Если значение функции в найденной точке лучше предыдущего, то движение продолжается в том же направлении, но с шагом, уменьшенным в соответствии со следующим правилом:
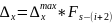
Лекция 7
Единственным слабым местом всех методов прямого поиска является требование унимодальности целевой функции. Целевая функция на интервале определенности должна иметь только один экстремум.
Методы нулевого порядка (многомерного поиска)
При решении практических задач, когда в реальном масштабе времени обрабатывается оперативная информация с объекта оптимизации, с целью нахождения оптимального решения, применение градиентных методов весьма затруднительна. Это объясняется тем, что направление градиента, при приближенном вычислении производных, может быть определено с большой погрешностью, это приводит к существенному возрастанию вычислительных затрат(потерь на поиск) и возможности появления ошибки в определении экстремума. Поэтому в таких случаях широкое применение получили методы нулевого порядка – безградиентные методы детерминированного поиска.
Метод Гаусса-Зейделя (метод поочередного варьирования переменных)
Суть метода заключается в следующем: в стартовой точке рассчитывается значение целевой функции и определяется очередность изменения варьирования переменных, для этого рассчитываются частные производные по всем независимым переменным (как и в методе релаксации). В первую очередь должна варьироваться та переменная, частная производная по которой по модулю максимальна. Очередность изменения переменных на последующих циклах не изменяется. По найденному направлению, с выбранным постоянным шагом, осуществляется движение до тех пор, пока целевая функция изменяется желательным образом:
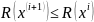
(условие для минимума)
При этом все остальные переменные зафиксированы. При нарушении данного условия необходимо вернуться на два шага назад и в найденном интервале неопределенности применить один из прямых методов одномерного поиска. После того как будет найден локальный экстремум по пройденному направлению, точка фиксируется и аналогичным образом осуществляется поиск локального экстремума по следующим переменным.
Поиск глобального экстремума заканчивается при выполнении выбранного критерия прекращения поиска. К трем общим добавляется специфический - количество циклов. Под циклом понимается тот момент, когда проварьированы все переменные. Таким образом, стратегия метода заключается в отыскании локального экстремума по каждой независимой переменной, при фиксированных значениях остальных.
Методы сканирования
Суть методов состоит в последовательно просмотре значений критерия оптимальности в ряде точек, принадлежащих области определения функции, при этом, чем гуще расположены точки внутри области, тем выше точность нахождения экстремума.
Применение методов позволяет со 100% гарантией найти глобальный экстремум, поскольку исследуется вся область определения функции. Наличие ограничений не усложняет поиск, а наоборот облегчает его, поскольку сужается область определения функции.
Существует три метода сканирования:
Метод с постоянным шагом.
Сканирование с переменным шагом.
Сканирование по спирали.