Методы, использующие градиент Метод градиента

В оптимизации применение градиента обусловлено его важнейшим свойством: направление градиента совпадает с направление скорейшего возрастания целевой функции. Поэтому в стартовой точке поиска рассчитываются частные производные целевой функции, которые являются составляющими вектора градиента и находится направление градиента.

Из найденной(стартовой) точки в направлении градиента осуществляется шаг, при котором изменяются обе переменные, каждая из них получает приращение, пропорциональное соответствующей частной производной.

Два алгоритма могут быть использованы при поиске экстремума:

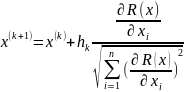
В данном алгоритме используется нормализованный вектор градиента, который не учитывает скорость возрастания целевой функции. Поэтому для повышения эффективности поиска может быть предложен следующий алгоритм изменения шага h_k :

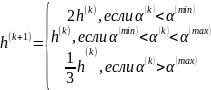
α^(k) – угол поворота градиента при переходе в следующее состояние. Этот угол может быть определен по следующему правилу:

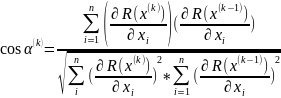
Лекция 6 Метод наискорейшего спуска

Методы одномерного поиска

Методы предназначены для отыскания экстремума функции одной переменной.

Формализация задачи сводится к нахождению такого значения переменной х, при которой значение функции принимает максимальное значение: f(x) → extr ; x принадлежит (a,b)

Эти методы распределяются на два класса: методы использующие производные и не использующие производные.

Методы не использующие производные называются методами прямого поиска. Основная идея, объединяющая все эти методы, заключается в отыскании точек на вещественной оси (а, b), в которых необходимо вычислить целевую функцию.

Специфика и особенность каждого метода прямого поиска заключается в способах отыскания этих точек.

Метод дихотомии (половинного деления)

Одним из параметров является Δ – малое число.

x₁=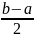

b*-a*<=ε

Метод локализации экстремума

Основная идея метода заключается в разбиении отрезка вещественной оси на N равных частей (N кратно четырем). В каждой найденной точке вычисляется значение целевой функции. Для дальнейшего рассмотрения выбирается сокращенный подинтервал , состоящий из двух отрезков, на общей границе которого целевая функция принимает экстремальное значение. Этот интервал подвергается такому же разбиению, но количество вычислений функции уменьшается вдвое, т.к. вычисляется значение функции только в точках х₄ и х₅.

Существует модификация метода, заключающаяся в том, что по информации о длине отрезка (a,b) выбирается шаг в 4 раза меньше его длины. С этим шагом осуществляется движение от любого из концов отрезка (a,b) до тех пор, пока функция изменяется желательным образом. Как только функция начинает изменяться в нежелательную сторону, направление движения меняется на противоположное, и шаг уменьшается в 4 раза.

Метод золотого сечения

z²-3z+1=0

z=0.38

Если в исходном делении отрезка (x₀,x₃) выбраны точки х₁ и х₂ таким образом, что они отстоят на расстоянии от границ отрезка по следующему правилу:

х₁=a+z(x₃-x₀)

x₂=b-z(х₃-х₀)

То в любом из подинтервалов (x₀,x₂) , либо (х₁,х₃) можно выбрать точку х₄ по соответствующему правилу, что деление нового подинтервала будет подобно предыдущему.

х₄=x₂-z(x₂-x₀)

Такое иррациональное деление отрезка позволяет существенно повысить эффективность поиска.