Общая характеристика методов нелинейного программирования
При решении любой оптимизационной задачи с помощью методов нелинейного программирования пользователь сталкивается с тремя основными проблемами:
Выбор стартовой или исходной точки. Выбор стартовой точки наиболее актуален при решении многоразмерной задачи оптимизации со сложными целевыми функциями. Очевидно, если стартовая точка находится в дали от экстремума, то затраты на поиск могут быть неоправданно высокими. Эта задача особо актуальна для оперативного управления технологическими процессами. При решении таких задач в качестве стартовой точки, как правило, может использоваться номинальный режим.
Выбор шага поиска. По своей сути все методы нелинейного программирования являются многошаговыми, т.е. методами последовательного улучшения исходного или промежуточного состояния. Заранее сказать, какое наименьшее количество шагов необходимо для отыскания экстремума с заданной точностью невозможно. Если шаг выбран постоянным, то, как правило, его значение слишком мало, если стартовая точка находится вдали от экстремума, если стартовая точка находится вблизи от экстремума, постоянное значение шага может привести к появлению рысканья в районе экстремума.
Адаптация значения шага конкретной характеристики поверхности требует существенного увеличения вычислительных затрат, что не всегда оправданно. Многообразие методов нелинейного программирования, их особенностей объясняется в задаче поиска оптимального значения шага. Все методы нелинейного программирования используют идею движения в n-мерном пространстве независимых переменных, при этом из некоторого промежуточного или исходного состояния x(k) осуществляется переход в следующее состояние x(k+1) путем изменения вектора x(k) на некоторую величину Δх(k), которая называется шагом поиска, иными словами, в самом общем виде, алгоритм любого метода нелинейного программирования может быть записан в следующем виде:
x(k+1)= x(k)+ Δх(k),
В ряде случаев шаг поиска может быть функцией текущего состояния объекта:
Δх(k)= Δх(k)(x(k)) , а так же рядом предыдущих состояний: Δх(k)= Δх(k)=( x(k), x(k-1), x(k-2))
Методы, в которых реализованы эти алгоритмы, являются более универсальными, поскольку в них используется информация о характере поведения целевой функции при движении к экстремуму.
Выбор критерия прекращения поиска. Существует три основных критерия прекращения поиска, которые нашли применение практически во всех оптимизационных методах.
Точность по функции – абсолютная разность между двумя значениями функции, полученными на предыдущем и текущем этапах поиска не превышает наперед заданной величины. |R(x(k))-R(x(k-1))|<=ε
Точность по координатам – абсолютная разность между двумя значениями координат на предыдущем и текущем этапах поиска не превышает заданной величины. | x(k)-x(k-1)|<=δ
Количество вычислений целевой функции.
Кроме того каждый из методов может иметь свой специфический критерий прекращения поиска.
Классификация методов нелинейного программирования
В зависимости от выбора шага и соответственно направления движения к экстремуму, методы нелинейного программирования разбиваются на следующие основные группы:
Методы нулевого порядка
Детерминированные
Методы случайного поиска
Методы первого порядка
Методы использующие градиент
Методы не использующие градиент
Методы второго порядка
Методы первого порядка
Методы не использующие градиент
Метод релаксации
Основная идея метода заключается в отыскании осевого направления, по которому целевая функция изменяется наиболее значительно. Для этого в стартовой точке поиска определяются частные производные целевой функции по всем независимым переменным, и находится переменная, по которой функция изменяется сильнее (ей соответствует максимальная по модулю производная). Далее идет движение до нахождения локального экстремума, в точке локального экстремума заново рассчитываются производные по всем независимым переменным, за исключением той, по которой осуществлялось движение. Условием прекращение оптимума может служить следующее:
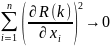
Иными словами поиск экстремума прекращается тогда, когда при любом направлении движения из найденной точки улучшения значения целевой функции не происходит. Алгоритм метода может быть записан в следующем виде:
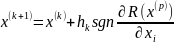
Для повышения эффективности поиска шаг поиска может изменяться по следующему алгоритму:
