Методы нелинейного программирования

Если критерий оптимальности представлен сложной нелинейной зависимостью или в явном виде отсутствует, а независимые переменные связаны между собой зависимостями, представленными равенствами, неравенствами или тем и другим вместе, то единственным способом решения таких оптимизационных задач является численный способ, реализуемый методами нелинейного программирования. Для формализации задачи нелинейного программирования используется векторное представление независимых переменных X=X(x₁, x₂,…х_n-1,x_n)

Тогда формализованная постановка задачи нелинейного программирования может быть представлена в следующем виде:

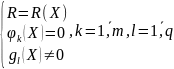
Целевая функция R(X) в пространстве независимых переменных x_i представленная некой поверхностью, поскольку наглядное изображение отсутствует, будем использовать двухмерное изображение.

Пересечение поверхности параллельными плоскостями дает нам семейство линий равного уровня, охватывающих точку экстремума. Проекция линий равного уровня на плоскость переменных позволяет получить нам семейство замкнутых (если целевая функция непрерывна) линий, так же охватывающих точку экстремума, называемых линиями равного значения целевой функции.

Особые точки целевой функции.

От вида целевой функции во многом зависит эффективность того или иного метода. Основные проблемы при оптимизации возникают с функциями, имеющими седловой и овражный характер.

Овражные точки

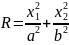, a>>b

Нормирование и масштабирование

При решении конкретных практических задач приходится манипулировать с переменными, имеющими разный физический смысл и соответственно различные размерности (температура, расход, давление и т.д.)

Для удобства решения задач оптимизации целесообразно использовать нормализованные значения независимых переменных. Обычно для нормализации используется возможные диапазон изменения переменных. Предположим, некоторая переменная y_i может изменяться в диапазоне от y_i^мин до y_i^макс. Обозначим этот диапазон через d и введем новую переменную x_i.

y_i^мин <y_i< y_i^макс

x_i= (y_i^макс- y_i^мин)/d

Возможный диапазон изменения переменной x_i : от 0 до 1.

Целевая функция может быть плохо масштабирована, т.е. от какой-то из переменных зависеть намного слабее, чем от других.

Пример:

R=100x₁²-0,01x₂²

Целевая функция от х1 и х2 намного слабее будет зависеть от второй переменной.

Одним из способов масштабирования является введение новых переменных.

Лекция 5 Глобальные и локальные экстремумы целевой функции

При отыскании оптимума целевой функции задачей является нахождение такой совокупности значений независимых переменных, которые обеспечивают действительно наибольшее или наименьшее значение функции, иными словами в точке оптимума обязательно должно выполняться условие:

R(x_опт)<=R(x) х принадлежит

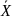
Которое справедливо для любогоx формирующего область определения функции. Такая точка называется глобальным экстремумом.

Кроме того целевая функция может иметь ряд точек x^(k), k=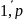 для которых вышеупомянутое условие справедливо лишь в окрестности этих точек. Такие оптимумы носят название локальных экстремумов.

Поскольку для сложных нелинейных функций вид поверхности установить сложно, становится очевидными трудности отыскания глобальных экстремумов. Одним из способов нахождения глобального экстремума является старт из разных начальных точек.