Методы исследования функций на базе классического анализа

Областью применения данных методов являются задачи, в которых критерий оптимальности или целевая функция представлен явным несложным аналитическим видом, что позволяет находить и анализировать также аналитические выражения для производных целевой функции. Ограничения на независимые переменные отсутствуют. Необходимым условием экстремума функции является равенство нулю первой производной или ее отсутствие. Равенство нулю или отсутствие первой производной является лишь необходимым условием наличия экстремума в точке. Поскольку функция может иметь такие точки ,в которых условие выполняется, а экстремума нет, поэтому получаемое при решении задачи условие обязательно должно быть проверено на достаточность. Существует три способа проверки.

1 Способ: исследование значений функции. При этом способе сравниваются значения функции, рассчитанные в точке подозрительной на экстремум и в двух точках, лежащих в ε-окрестности этой точки.

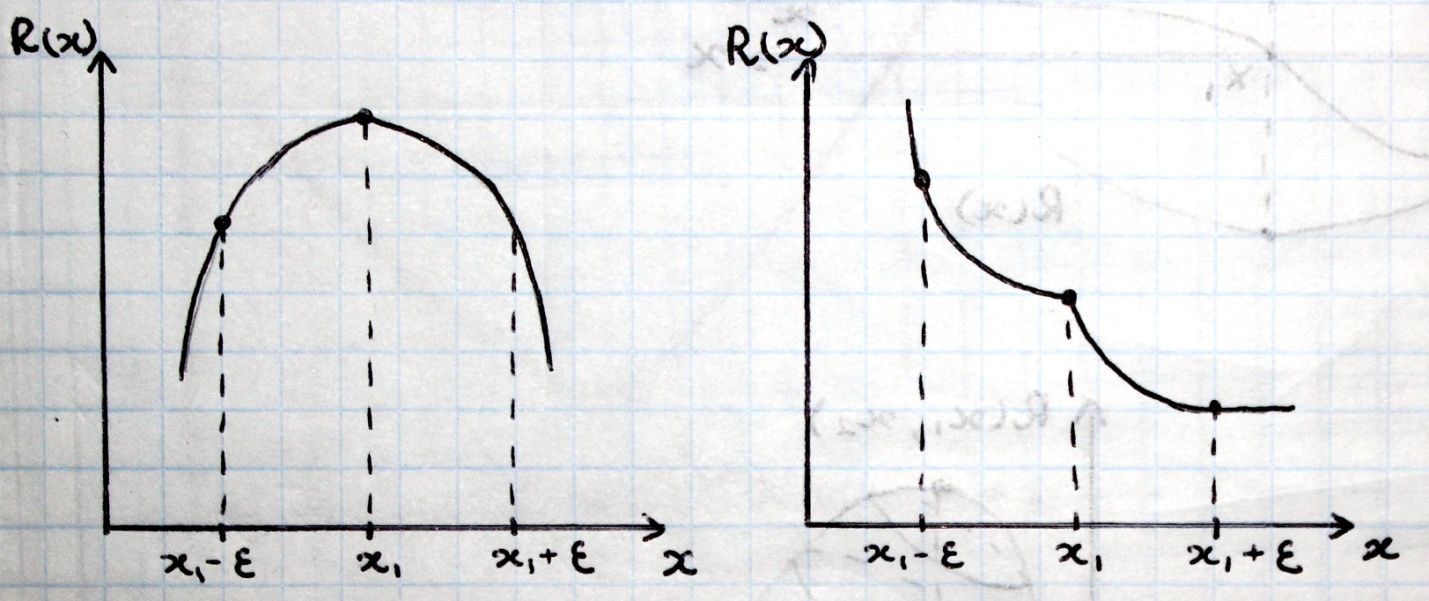
2 Способ: исследование знаков первой производной, суть способа заключается в сравнении знаков производной в окрестности точки подозрительной на экстремум. Если производные имеют разные знаки, экстремум в точке имеется.

3 Способ: сравнение знаков высших производных. Применение данного способа проверки на достаточность подразумевает, что целевая функция непрерывна сама и имеет также непрерывные первую и более высокого порядка производную.

Достаточным условием наличия экстремума в точке является неравенство нулю второй производной. О типе экстремум судят по знаку второй производной: отрицательная в точке максимума, положительная в точке минимума. Для наличия экстремума необходимо, чтобы четная производная была отлична от нуля.

Лекция 4

Задача во многом усложняется, если функция зависит от нескольких переменных. Особые проблемы возникают при отсутствии непрерывности первых производных по некоторым переменным, в этом случае оптимизационная задача может быть решена только численным способом. Если все первые производные целевой функции по всем независимым перемененным в точке x_i^k подозрительной на экстремум непрерывны, то необходимым условием наличия экстремума в этой точке будет равенство нулю этих производных. Иными словами, для проверки необходимости требуется решить следующую систему дифференциальных уравнений в частных производных.

Для многомерной задачи оптимизации проверка решения на достаточность является весьма проблематичной, поскольку целевая функция может иметь такой характер, когда по одной переменной функция имеет максимум, а во второй минимум, т.е. функция имеет седловой характер.

Для решения задачи оптимизации таких функций может применяться следующий подход: в окрестности «подозрительной» точки целевая функция раскладывается в ряд Тэйлора по приращению Δх_i и проверяется условие Сильвестра.

Методы исследования функций на базе классического анализа являются основой всех оптимизационных методов.

Методы с использованием неопределенных множителей Лагранжа.

Существует большое количество практических задач, в которых необходимо оптимальным образом распределить заданное количество ресурсов, т.е. решить задачу оптимизации, при наличии ограничений на независимые переменные, записанных в виде равенств.

Предположим, что целевая функция: R=R(x_i) -> ext2

i=1,n

Её независимые переменные x_i взаимосвязаны с собой в виде функциональной зависимости:

Φ_k(x_i)=0, k=1,m

Достаточно просто задача оптимизации решается, если ее размерность n равна количеству ограничений m. В этом случае задача сводится к поиску определенного набора дискретных значений x_i путем решения системы Φ_k(x_i)=0, при подстановке которого в значение целевой функции можем найти ее оптимальное значение. В иных случаях (n не равно m) применяется метод Лагранжа, его суть заключается в следующем:

Каждое из ограничений Φ_k(x_i)=0 домножается на неопределенные множители λ_k и формируется новая целевая функция Φ(х, λ), называемая функцией Лагранжа:

Φ(х, λ)=R(x)+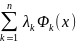

Решение задачи оптимизации в дальнейшем связано с нахождением таких x и λ, которые обращают в 0 частные производные функции Лагранжа по всем независимым переменным. Иными словами должна быть решена система уравнений:

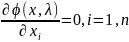
Полученное решение системы обязательно должно быть проверено на достаточность.