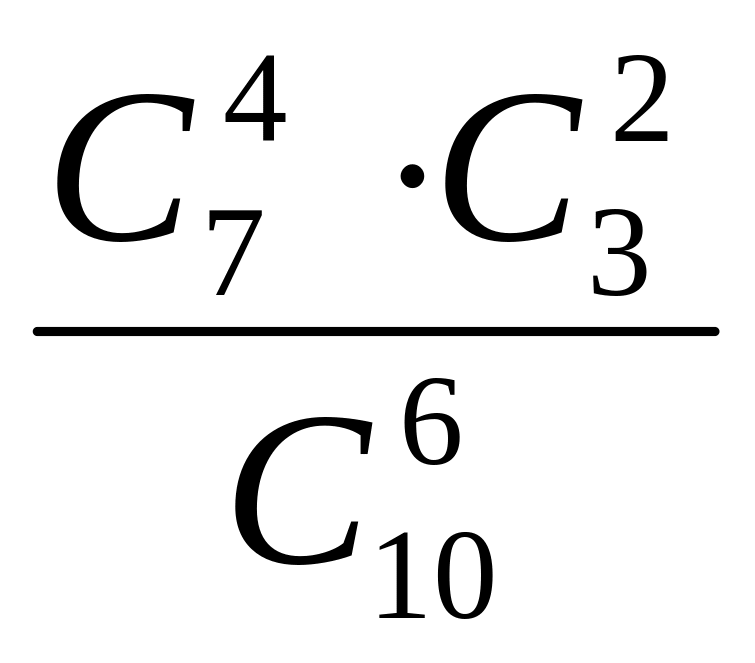2.2. Практические задания

2.2.1. В урне 5 белых и 4 черных шара, различающихся только цветом.

1) Вынимают наудачу один шар. Найти вероятность того, что он белый.

2) Вынимают наудачу два шара. Найти вероятность того, что:

а) оба шара белые;

б) хотя бы один из них черный.

2.2.2. У продавца на рынке 60 арбузов, из которых 50 спелых. Покупатель выбирает 2 арбуза. Какова вероятность того, что оба арбуза спелые?

2.2.3. В универмаге были проданы 27 магнитофонов трех марок «Samsung», «Panasonic» и «Toshiba», имеющихся в количествах 6, 8 и 16 штук. Полагая, что каждый магнитофон имеет одинаковую возможность быть проданным, найдите вероятность того, что остались непроданными магнитофоны:

а) одной марки;

б) трех разных марок.

2.2.4. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей:

а) нет бракованных;

б) нет годных.

2.2.5. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.

2.2.6. Студент пришел на экзамен, зная лишь 24 из 32 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент ответит на все вопросы.

2.2.7. Из 15 билетов выигрышными являются четыре. Какова вероятность того, что среди взятых наудачу шести билетов будет два выигрышных?

2.2.8. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.

2.2.9. По цели произведено 20 выстрелов, причем зарегистрировано 18 попаданий. Найти относительную частоту попаданий в цель.

2.2.10. На отрезок АВ длины  наудачу нанесена точка С, Найти вероятность того, что меньший отрезок из отрезков АС и СВ имеет длину, большую, чем .

2.2.11. Два студента условились встретиться в определенном месте межу 12 и 13 часами дня. Пришедший первым ждет второго в течение ¼ часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).

Тесты по теме

1. В ящике 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

1) 2) 3) 4) нет ответа

2. Бросают одна за другой две кости. Вероятность того, что сумма очков будет равна 10.

1) 2) 3) 4) 5) Ответ не указан

3. В конверте среди 100 фотографий находится одна разыскиваемая. Из конверта наугад выбирается 10 фотографий. Найти вероятность того, что среди извлеченных окажется нужная.

1) 2) 3) 4) Нет ответа

4. Вероятность случайного события есть положительное число, равное:

1) 1 2) 0 3) 0 Р(а) 1 4) нет ответа

5. В ящике 10 красных и 6 синих пуговиц. Какова вероятность, что две наудачу вынутые пуговицы будут синими.

1) 6/10 2) 2/10 3) 4)

6. В партии из 10 деталей 7 стандартных найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.

1)1/3 2) 4/17 3) 4)