Тема 10. Некоторые законы распределения непрерывных случайных величин.

10.1.Контрольные вопросы

1. Непрерывная случайная величина Х имеет равномерный закон распределение вероятностей на отрезке [a;b]. Запишите, какой вид имеет ее плотность распределения вероятностей и функция распределения вероятностей. Изобразите графики этих функций.

2. Запишите формулы для нахождения математического ожидания и дисперсии НСВ, распределенной равномерно:

М(Х) =

D(X) =

3. Непрерывная случайная величина Х имеет показательный или экспоненциальный закон распределение вероятностей. Запишите, какой вид имеет ее плотность распределения вероятностей и функция распределения вероятностей. Изобразите графики этих функций.

4. Запишите формулы для нахождения математического ожидания и дисперсии НСВ, распределенной по показательному закону:

М(Х) =

D(X) =

5. Непрерывная случайная величина Х имеет нормальный закон распределение вероятностей. Запишите, какой вид имеет ее плотность распределения вероятностей и функция распределения вероятностей. Изобразите графики этих функций.

6. Случайная величина Х имеет нормальное распределение с параметрами а и σ. Запишите в чем заключается вероятностный смысл этих параметров.

7. Запишите формулу для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от α до β.

8. Перечислите свойства интегральной функции Лапласа.

9. В чем состоит правило трех сигм?

10.2. Практические задания по теме.

Задача 10.2.1. На перекрестке дорог движение регулируется автоматическим светофором, включающим зеленый свет через каждые 2 мин. Время простоя автомобиля у этого светофора, про­ехавшего на красный свет, есть случайная величина, распре­деленная равномерное с плотностью на участке 0 - 2 мин. Найдите среднее время простоя и среднее квадратическое отклонение.

Задача 10.2.2. В здании областной администрации случайное время ожидания лифта равномерно распределено в диапазоне от 0 до 5 мин.

а) Чему равна функция распределения F(x) для этого равномерного распределения?

б) Чему равна вероятность ожидания лифта более чем 3,5 мин?

в) Чему равна вероятность того, что лифт прибудет в течение первых 45 сек?

г) Чему равна вероятность, что время ожидания лифта в диапазоне от 1 до 3 мин (между 1 и 3 мин)?

Задача 10.2.3. Случайная величина X, распределенная равномерно, имеет следующие числовые характеристики М(X) = 2, D(X) = 3. Найти F(x).

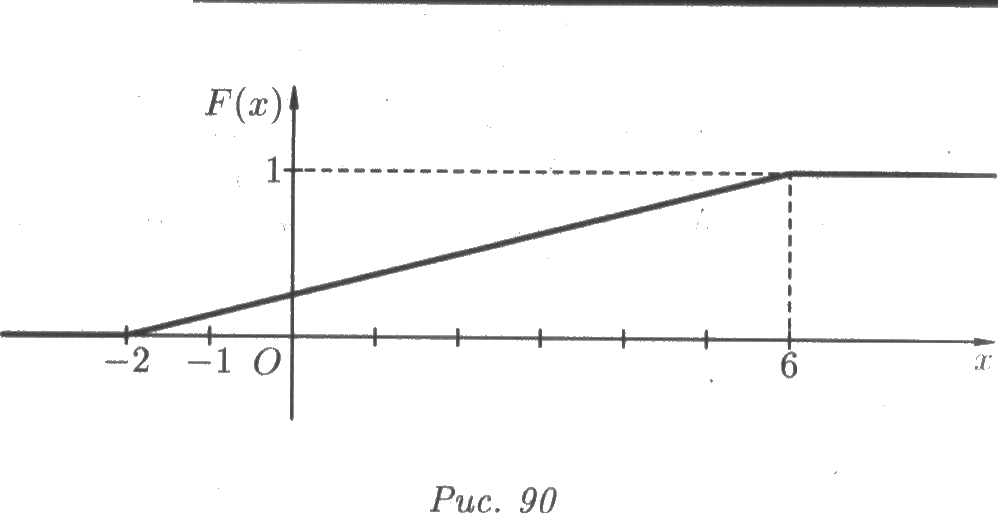
Задача 10.2.4. Функция распределения непрерывной случайной величины X имеет вид, указанный на рисунке. Найти аналитические выра­жения для F(x), f(x), M(X) и D(X).

Задача 10.2.5. Служащий рекламного агентства утверждает, что время, в течение которого телезрители помнят содержание коммерче­ского рекламного ролика, подчиняется экспоненциальному закону с  = 0,25 дня. Найдите вероятность того, что зрители вспом­нят рекламу спустя 7 дней?

Задача 10.2.6. Время Т выхода из строя радиостанции подчинено показательному закону распределения с плотностью

Найти: функцию распределения; математическое ожидание и дисперсию случайной величины Т; вероятность того, что радиостанция сохранит работоспособность от 1 до 5 час. работы.

Задача 10.2.7. Случайная величина X распределена по показательному закону с параметром  = 0,4. Найти дифференциальную и интегральную функцию распределения, а также вероятность попадания значений СВХ в интервал (0,25; 5).

Задача 10.2.8. Срок службы жесткого диска компьютера — случайная величина, подчиняющаяся экспоненциальному распределению со средней в 12 000 ч. Найдите вероятность того, что срок службы жестких дисков превысит 20 000 ч.

Задача 10.2.9. Еженедельный выпуск продукции на заводе распределен приблизительно по нормальному закону со средним значением, а=134786 ед. продукции в неделю и σ=13000ед. Найдите вероятность того, что еженедельный выпуск продукции:

а) превысит 150 000 ед.;

б) окажется ниже 100 000 ед. в данную неделю.

Задача 10.2.10. Пусть X — нормально распределенная случайная величина с математическим ожиданием а = 16 и со средним квадрати­ческим отклонением σ = 3. Найдите:

а) Р(11 <Х<20);

6) Р(17<Х<49).

Задача 10.2.11. Рост взрослых мужчин является случайной величиной Х, распределенной по нормальному закону: X ~ N (175;10). Haйти плотность вероятности, функцию распределения этой случайной величины; вероятность того, что ни один из 3 наудачу выбранных мужчин не будет иметь рост менее 180 см.

Задача 10.2.12. Случайная величина X является нормально распределенной. Ее математическое ожидание равно 40, а вероятность ее попадания в интервал (36;44) равна 0,966. Найти среднее квадратическое отклонение случайной величины.

Задача 10.2.13.Заданы математическое ожидание а и среднее квадратическое отклонение  нормально распределенной случайной величины Х. Найти 1) вероятность того, что случайная величина Х примет значение, принадлежащее интервалу (;); 2) вероятность того, что абсолютная величина отклонения Х – а окажется меньше ; 3) интервал, в который попадут значения случайной величины с вероятностью 0,9836.

а=15; =2; =9; =19; =3.

Задача 10.2.14. Месячный доход семей можно рассматривать как случайную величину, распределенную по нормальному закону с математическим ожиданием М(Х)= 4000руб. и средним квадратическим отклонением σ(Х)=800руб. Какова вероятность, что из трех семей, по крайней