2. Практические задания по теме:
Задание 1. Для функции у=f(x) указаны и точке х0 односторонние пределы и значение функции в ней. Исследовать функцию на непрерывность в точке х0 и устанавливать характер точки разрыва, если он есть:
а)
f(x0)=2,
;
__________________________________________________________________
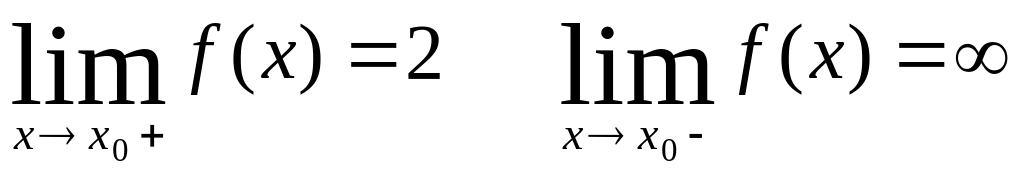б)
;
__________________________________________________________________
в)
;
__________________________________________________________________
г)
____________________________________________________________________________________________________________________________________
Задание 2. Выяснить, какие из функций непрерывны в точке х=2 (ответ обосновать);
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задание 3. Исследовать функцию на непрерывность и найти точки разрыва функции (указать их характер):
1. Находим область определения:
__________________________________________________________________
2. Рассмотрим поведение функции в точках_____________________________
а) х=__, найдём предел функции в ней _________________________________
_____________, значит х=___ точка разрыва _______________________рода;
б) х=__, найдём предел функции в ней _________________________________
значит х=__ точка _________________разрыва.
1. Находим область определения:
__________________________________________________________________2. Рассмотрим поведение функции в точках х=___,т. к. в ней функция изменяет своё поведение. Найдём односторонние пределы.
_______________________________,значит х=__ точка разрыва ____рода.
3. Задания для самостоятельной работы
Исследовать функцию на непрерывность и найти точки разрыва функции (указать их характер):
1. 
___________________________________________________________________________________________________________________________
2. 
______________________________________________________________________________________________________________________________________________________________________________________________________
3. 
______________________________________________________________________________________________________________________________________________________________________________________________________
4.
______________________________________________________________________________________________________________________________________________________________________________________________________
5.
_____________________________________________________________________________________________________________________________________________________________________________________________________
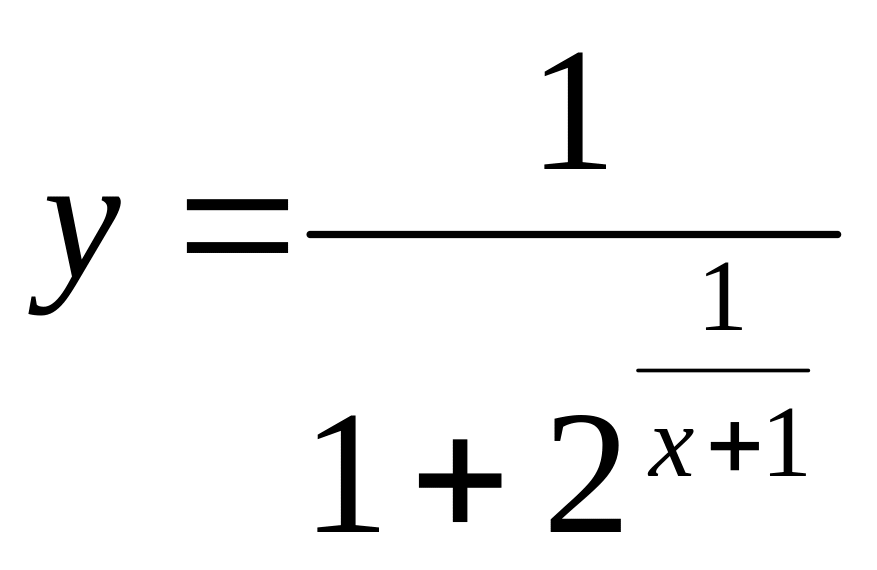
6.
______________________________________________________________________________________________________________________________________________________________________________________________________
7.
______________________________________________________________________________________________________________________________________________________________________________________________________
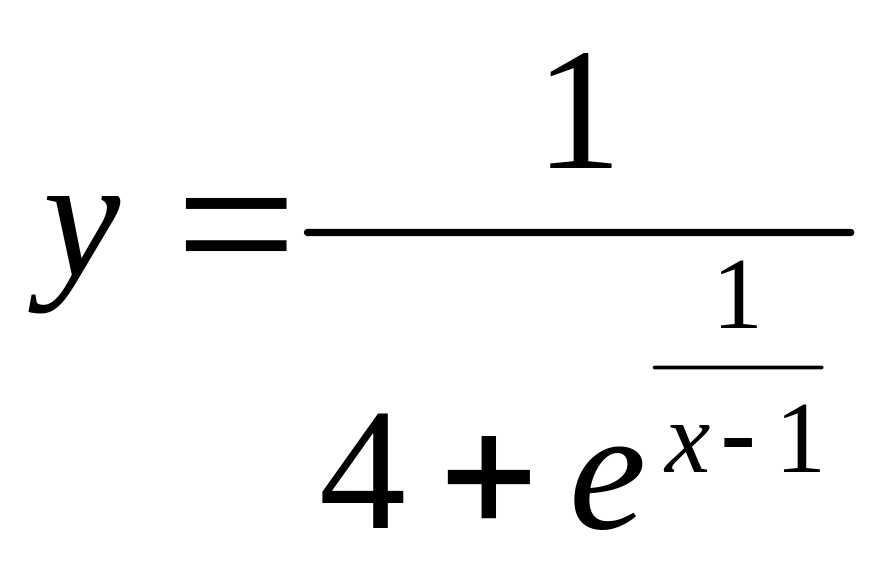
8. 
______________________________________________________________________________________________________________________________________________________________________________________________________